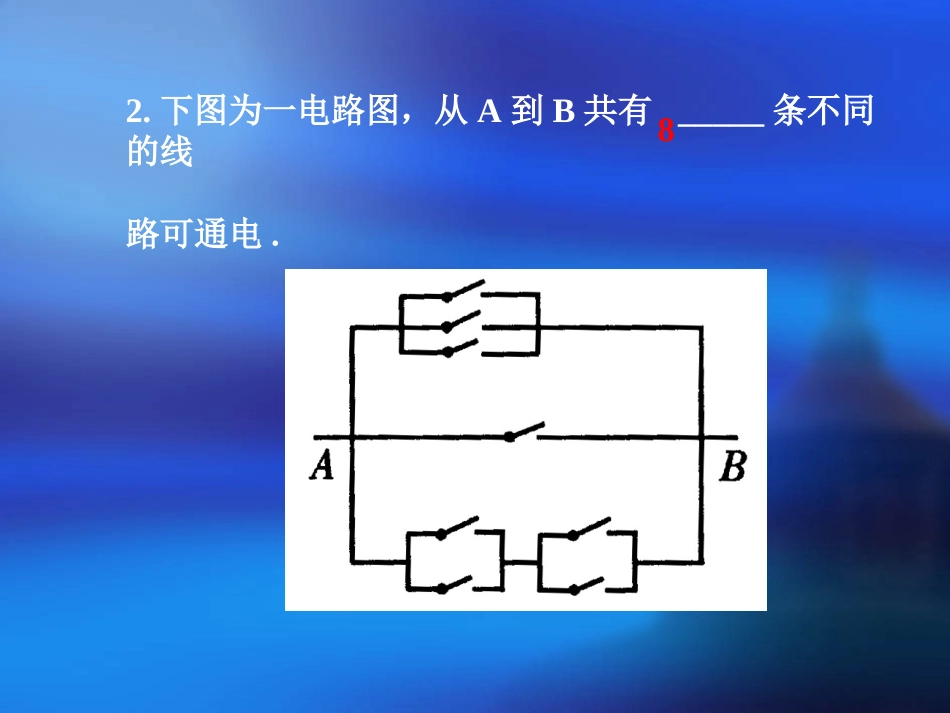
第1节排列与组合(一)要点要点··疑点疑点··考点考点!!!nAm-nnAnnmn,1.1!!!0nnnrnCCrr-nnC,2.课前热身1.++可能的值的个数为可能的值的个数为(()(A)1(B)2)(A)1(B)2(C)3(D)(C)3(D)无数个无数个BB110rC1710rC2.下图为一电路图,从A到B共有_____条不同的线路可通电.83.语、数、外三科教师都布置了作业,在同一时刻4名学生都做作业的可能情形有()(A)43种(B)34种(C)A34种(D)C34种B4.现从某校5名学生干部中选出4个人分别参加宿迁市“资源”、“生态”、“环保”三个夏令营,要求每个夏令营活动至少有选出的一人参加,且每人只参加一个夏令营活动,则不同的参加方案的种数是____.1805.不大于1000的正整数中,不含数字3的正整数的个数是()(A)72(B)648(C)729(D)728B【解题回顾】解法1先分类再分步,解法2分步结合排除法.可见对同一问题有时既可按元素性质分类思考,也可从事件过程分步思考.能力能力··思维思维··方法方法1.有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?(1)甲不在中间也不在两端;(2)甲、乙两人必须排在两端;(3)男、女生分别排在一起;(4)男女相间;(5)甲、乙、丙三人从左到右顺序保持一定.【解题回顾】本题集排列多种类型于一题,充分体现了元素分析法(优先考虑特殊元素),位置分析法(优先考虑特殊位置)、直接法、间接法(排除法)、捆绑法、等机会法、插空法等常见的解题思路.2.由0,1,2,3,4,5这六个数字,(1)能组成多少个无重复数字的四位数?(2)能组成多少个无重复数字的四位偶数?(3)组成无重复数字的四位数中比4032大的数有多少个?【解题回顾】①注意题中隐含条件零不能在首位;②由零不能在首位的隐含条件导致(3)必须分类求解.3.从4名男生,3名女生中选出3名代表.(1)不同的选法共有多少种?(2)至少有一名女生的不同选法共有多少种?(3)代表中男、女生都要有的不同选法共有多少种?【解题回顾】选举问题是一种典型的组合问题,常见的附加条件是分类选元.在解(2)、(3)时易犯的错误是重复选,如解(2)为C13C26=45种,解(3)为C13C14C15=60种.4.有11名外语翻译人员,其中5名英语翻译员,4名日语翻译员,另两名英、日语都精通,从中找出8人,使他们组成两个翻译小组,其中4人翻译英文,另4人翻译日文,这两个小组能同时工作,问这样的分配名单共可开出几张?【解题回顾】首先注意分类方法,体会分类方法在解组合问题中的作用.本题也可以先安排翻译英文人员,后安排翻译日文人员进行分类求解,共有C45C46+C35C12C45+C25C22C44=185种.5.8名世界网球顶级选手在上海大师赛上分成两组,每组各4人,分别进行单循环赛,每组决出前两名,再由每组的第一名与另一组的第二名进行淘汰赛,获胜者角逐冠亚军,败者角逐第3、4名,大师赛共有多少场比赛.延伸延伸··拓展拓展【解题回顾】要搞清各种比赛的规则:所谓单循环【解题回顾】要搞清各种比赛的规则:所谓单循环赛,是指同组中每个队与其他队均只进行一场比赛,赛,是指同组中每个队与其他队均只进行一场比赛,淘汰赛是指每场比赛都淘汰一名选手淘汰赛是指每场比赛都淘汰一名选手..6.央电视台“正大综艺”节目的现场观众来自四个单位,分别在图中4个区域内坐定.有4种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否则不受限制,那么不同的着装方法共有多少种?【解题回顾】当某种元素的不同限制条件对其他元素产生不同的影响时,应以此元素的不同限制条件作为分类的标准进行讨论.误解分析误解分析问题1:是排列还是组合?假期中全班40名同学都分别给同学写一封信,则共有多少封信?开学时,同班同学见面分别握一次手,共握手多少次?误解都是C240正解前者讲次序,是排列问题,答案为A240,后者不讲次序,是组合问题,答案为C240.问题2:在100件产品中有次品3件,正品97件,从中抽取4件,问至少抽得一件次品的方法数是多少?误解从3件次品中抽取1件,再从余下来的2件次品和97件正品(共99件)中任意抽取3件,即C13·C399.正解上述解法是一种正确的“操作”,但得到的是错误的答案,因为抽法违背了...