高考数学总复习 第2章第4课时函数的奇偶性与周期性精品课件 文 新人教A版 课件VIP免费

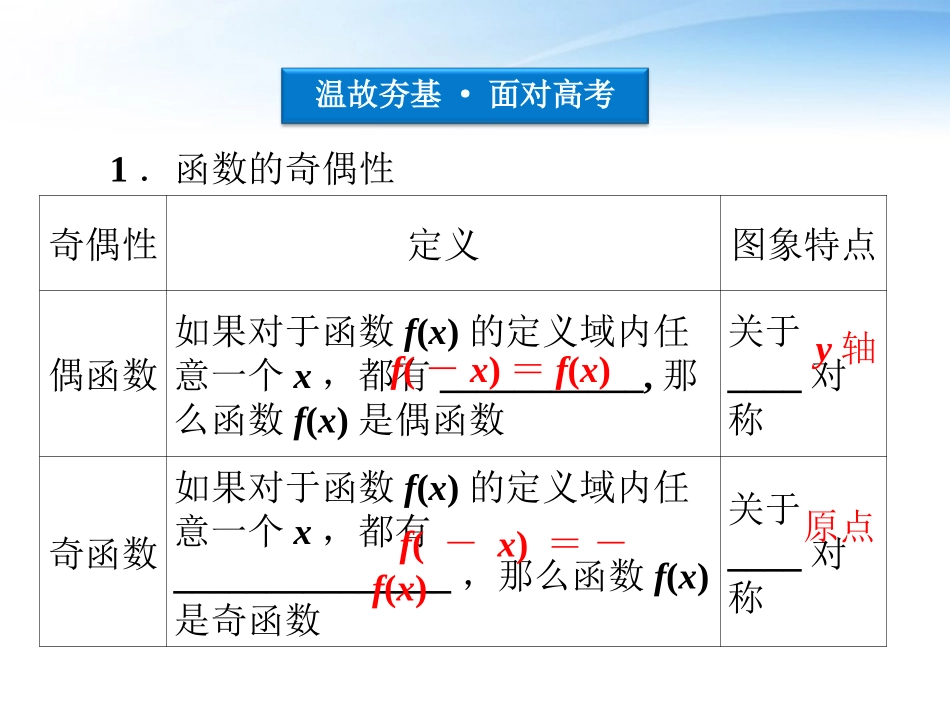
第4课时函数的奇偶性与周期性第课时函数的奇偶性与周期性4考点探究·挑战高考考向瞭望·把脉高考温故夯基·面对高考奇偶性定义图象特点偶函数如果对于函数f(x)的定义域内任意一个x，都有___________,那么函数f(x)是偶函数关于____对称奇函数如果对于函数f(x)的定义域内任意一个x，都有_______________，那么函数f(x)是奇函数关于____对称温故夯基·面对高考1．函数的奇偶性f(－x)＝f(x)y轴f(－x)＝－f(x)原点思考感悟奇、偶函数的定义域有何特点？提示：若函数f(x)具有奇偶性，则f(x)的定义域关于原点对称．反之，若函数的定义域不关于原点对称，则该函数无奇偶性．2．周期性(1)周期函数：对于函数y＝f(x)，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f(x＋T)＝______，那么就称函数y＝f(x)为周期函数，称T为这个函数的周期．(2)最小正周期：如果在周期函数f(x)的所有周期中_____________的正数，那么这个______正数就叫做f(x)的最小正周期．f(x)存在一个最小最小考点探究·挑战高考判断函数的奇偶性，应该首先分析函数的定义域，在分析时，不要把函数化简，而要根据原来的结构去求解定义域，如果定义域不关于原点对称，则一定是非奇非偶函数．函数奇偶性的判定考点突跛考点突跛例例11判断下列各函数的奇偶性．(1)f(x)＝lgx2＋lg1x2；(2)f(x)＝(x－1)1＋x1－x；(3)f(x)＝x2＋x，x<0－x2＋x，x>0；(4)f(x)＝lg1－x2|x－2|－2.【思路分析】可从定义域入手，在定义域关于原点对称的情况下，考查f(－x)与f(x)的关系．【解】(1)函数的定义域：(－∞，0)∪(0，＋∞)关于原点对称，且f(x)＝lg(x2·1x2)＝0(x≠0)．∴f(x)既是奇函数又是偶函数．(2)由1＋x1－x≥0得定义域为[－1,1)，关于原点不对称，故f(x)为非奇非偶函数．(3)当x<0时，－x>0，则f(－x)＝－(－x)2－x＝－(x2＋x)＝－f(x)；当x>0时，－x<0，则f(－x)＝(－x)2－x＝x2－x＝－f(x)．综上，对x∈(－∞，0)∪(0，＋∞)，都有f(－x)＝－f(x)．∴f(x)为奇函数．(4)易知f(x)的定义域是(－1,0)∪(0,1)，∴f(x)＝－lg1－x2x，f(－x)＝－f(x)．∴f(x)是奇函数．【名师点评】对于(1)的结论不能只说奇函数或偶函数．对于(2)若化简为f(x)＝－1－x2或者f(x)＝1－x2都导致错误判断．对于(3)要分段研究，不能只研究一段．对于(4)化简为等价变形．互动探究1若例1第(4)小题改为f(x)＝lg1－x2|x|－2，判断其奇偶性．解： 1－x2＞0|x|－2≠0，∴－1＜x＜1.∴函数定义域关于原点对称． f(－x)＝lg[1－－x2]|－x|－2＝lg1－x2|x|－2＝f(x)，∴函数f(x)是偶函数．(1)奇函数的图象关于原点对称；偶函数的图象关于y轴对称．(2)奇函数在关于原点对称的区间上的单调性相同，偶函数在关于原点对称的区间上的单调性相反．函数奇偶性的应用例例22已知奇函数f(x)的定义域为[－2,2]，且在区间[－2,0]内递减，求满足：f(1－m)＋f(1－m2)<0的实数m的取值范围．【思路分析】【解】 f(x)的定义域为[－2,2]．∴有－2≤1－m≤2－2≤1－m2≤2，解得－1≤m≤3.①又f(x)为奇函数，且在[－2,0]上递减，∴在[－2,2]上递减，∴f(1－m)<－f(1－m2)＝f(m2－1)⇒1－m>m2－1，即－2|m|－2≤1－m≤2－2≤m≤2，解得－1≤m<12.与奇函数、偶函数有关的求周期函数解析式问题，求解时将x设在所求解析式的区间上，将x加上或减去周期的倍数，转化为已知解析式的区间，利用奇、偶函数和周期函数的性质求出解析式．函数的周期性例例33(2011年梅州调研)设f(x)是定义在R上的奇函数，且对任意实数x，恒有f(x＋2)＝－f(x)．当x∈[0,2]时，f(x)＝2x－x2.(1)求证：f(x)是周期函数；(2)当x∈[2,4]时，求f(x)的解析式；(3)计算f(0)＋f(1)＋f(2)＋...