高三数学 7.5空间几何体及其表面积与体积复习课件2 课件VIP免费

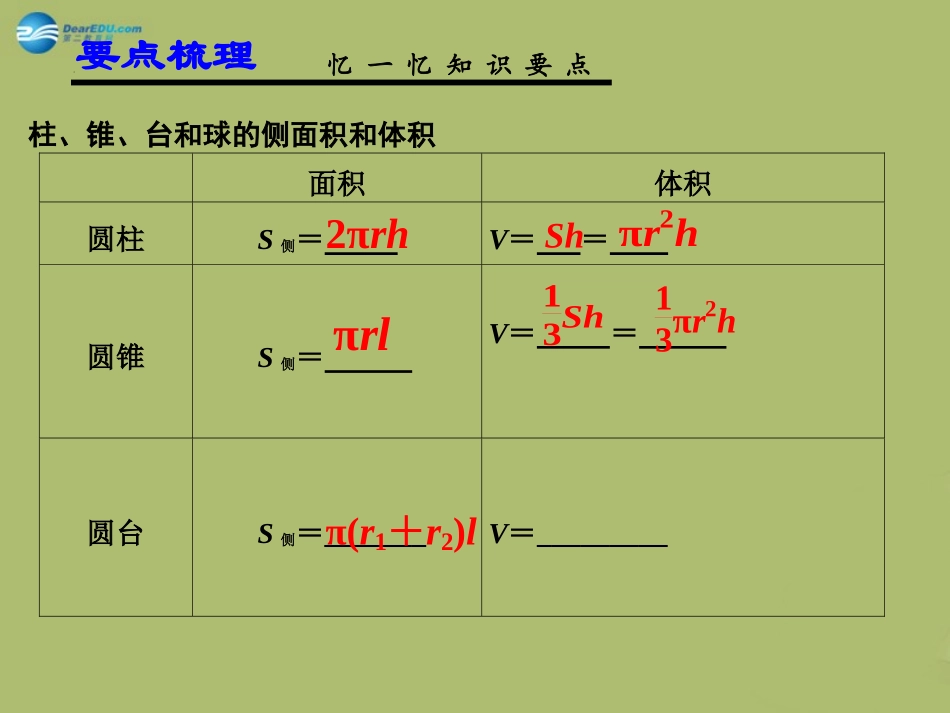
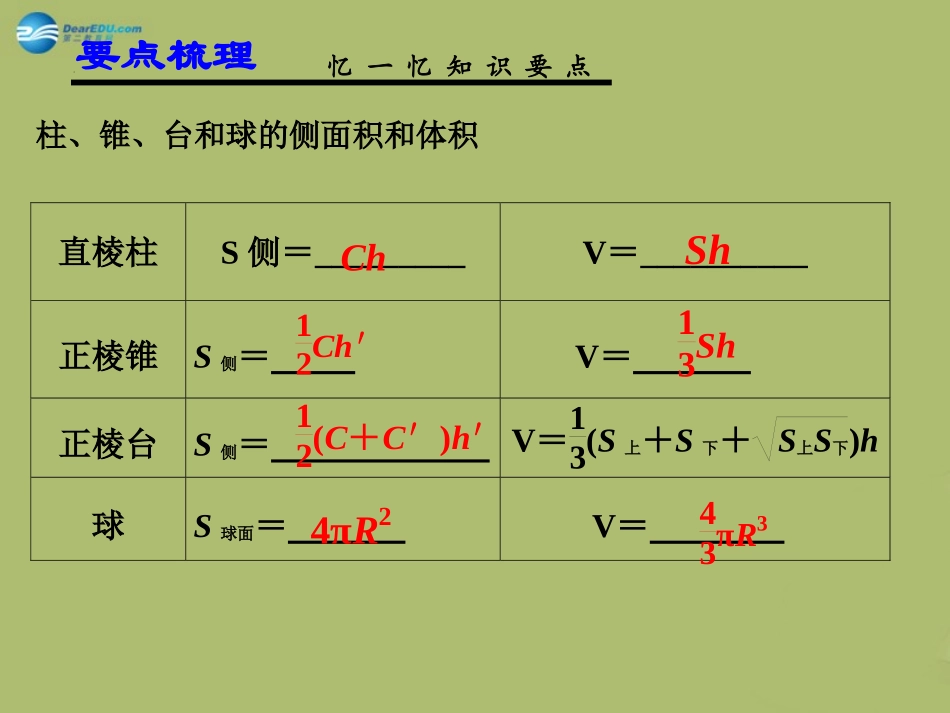
一轮复习讲义一轮复习讲义空间几何体及其表面积与体积柱、锥、台和球的侧面积和体积面积体积圆柱S侧＝V＝＝圆锥S侧＝V＝＝圆台S侧＝_______V＝_________忆一忆知识要点2πrhπrlShπr2h13Sh13πr2hπ(r1＋r2)l要点梳理直棱柱S侧＝_________V＝__________正棱锥S侧＝V＝正棱台S侧＝V＝13(S上＋S下＋S上S下)h球S球面＝V＝忆一忆知识要点12Ch′13Sh12(C＋C′)h′4πR243πR3要点梳理柱、锥、台和球的侧面积和体积ChSh一个正三棱台的上、下底面边长分别是3cm和6cm，高是32cm.(1)求三棱台的斜高；(2)求三棱台的侧面积和表面积．例3.基本元素的计算基本元素的计算已知一个正三棱台的两底面边长分别为30cm和20cm，且其侧面积等于两底面面积之和，求棱台的高．跟踪练习：(2013全国Ⅰ)如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器的厚度，则球的体积为A.500π3cm3B.866π3cm3C.1372π3cm3D.2048π3cm3A例4.题型三：表面积与体积的计算变式2.底半径为1,高为3的圆锥，其内接圆柱的底半径为R，当内接圆柱的体积最大时，R＝________.ABSO变式3.已知S、A、B、C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝AB＝1，BC＝2，则球O的表面积等于________．变式4.设三棱柱的侧棱垂直于底面，所有棱长都为a，顶点都在一个球面上，则该球的表面积为（）(A)2a(B)273a(C)2113a(D)25a变式5：（09全国）直三棱柱111ABCABC的各顶点都在同一球面上，若12ABACAA,120BAC，则此球的表面积等于．O20π23BC2324,sin120r222125,R24π20π.SR解析解析题型四角度问题例5.（2013大纲版理）已知正四棱柱1111ABCDABCD中12AAAB,则CD与平面1BDC所成角的正弦值等于（）A．23B．33C．23D．13变式6.（2013山东）已知三棱柱111ABCABC的侧棱与底面垂直,体积为94,底面是边长为3的正三角形.若P为底面111ABC的中心,则PA与平面ABC所成角的大小为（）A．512B．3C．4D．6OABCO补例：已知过球面上三点A,B,C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=2cm,则球的表面积是_________．解:如图,设球O半径为R,截面⊙O′的半径为r,,2ROOABC是正三角形，△4.3R22223Rt()(),23ROOAR在中,2166444.99SR323.33OAAB649πB组2．(2012·课标全国)已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为()A.26B.36C.23D.223．已知三棱锥A—BCD的所有棱长都为2，则该三棱锥的外接球的表面积为________．4．(2013·江苏)如图，在三棱柱A1B1C1－ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F－ADE的体积为V1，三棱柱A1B1C1－ABC的体积为V2，则V1∶V2＝________.半径为R的半圆卷成一个圆锥，则它的体积为．33π24RABSO当堂检测变式：将边长为a的正方形ABCD沿对角线AC折起，使BD=a，则三棱锥D—ABC的体积为（）A．63aB．123aC．3123aD．3122aC