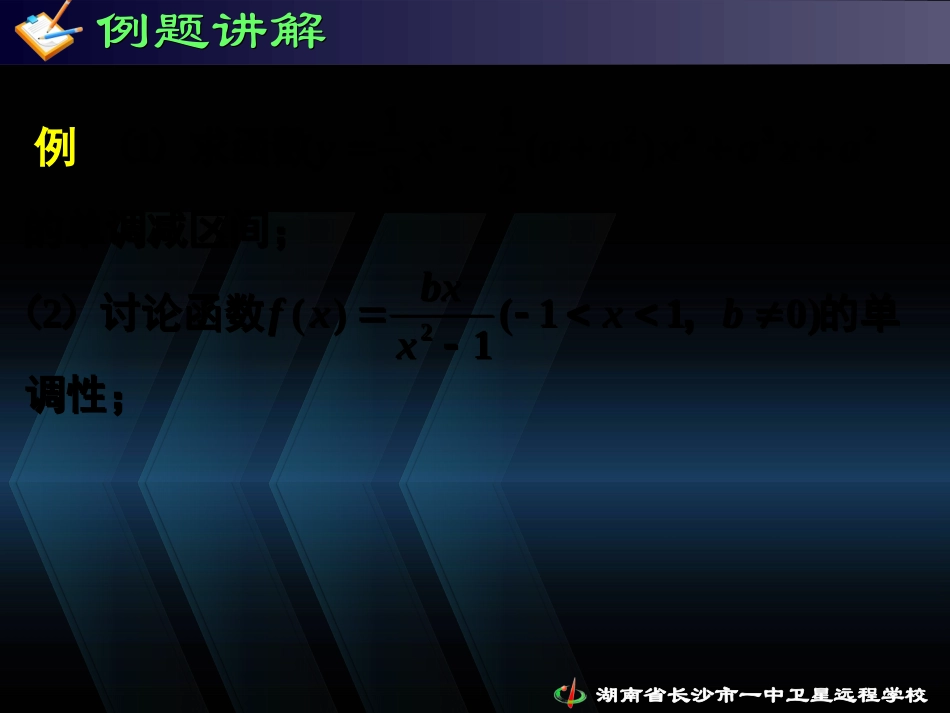
湖南省长沙市一中卫星远程学校主讲:陈震主讲:陈震湖南省长沙市一中卫星远程学校的单调减区间;)求函数(23223)(21311axaxaaxy的单调减区间;)求函数(23223)(21311axaxaaxy例题讲解例题讲解例例湖南省长沙市一中卫星远程学校的单调减区间;)求函数(23223)(21311axaxaaxy的单调减区间;)求函数(23223)(21311axaxaaxy例题讲解例题讲解例例调性;的单,)讨论函数()011(1)(22bxxbxxf调性;的单,)讨论函数()011(1)(22bxxbxxf湖南省长沙市一中卫星远程学校的单调减区间;)求函数(23223)(21311axaxaaxy的单调减区间;)求函数(23223)(21311axaxaaxy.)(1)1ln()1()(3的单调区间求,,其中)设函数(xfaxaaxxf.)(1)1ln()1()(3的单调区间求,,其中)设函数(xfaxaaxxf例题讲解例题讲解例例调性;的单,)讨论函数()011(1)(22bxxbxxf调性;的单,)讨论函数()011(1)(22bxxbxxf湖南省长沙市一中卫星远程学校例题讲解例题讲解题型一:求参数的取值范围题型一:求参数的取值范围湖南省长沙市一中卫星远程学校.]3(2)1(3)(2的取值范围上是减函数,求实数,在区间要使函数axaxxf.]3(2)1(3)(2的取值范围上是减函数,求实数,在区间要使函数axaxxf例题讲解例题讲解例1.例1.题型一:求参数的取值范围题型一:求参数的取值范围湖南省长沙市一中卫星远程学校.]3(2)1(3)(2的取值范围上是减函数,求实数,在区间要使函数axaxxf.]3(2)1(3)(2的取值范围上是减函数,求实数,在区间要使函数axaxxf例题讲解例题讲解例1.例1.题型一:求参数的取值范围题型一:求参数的取值范围.)6()41(1)1(2131)(23的取值范围实数上是增函数,求,上是减函数,在区间,在区间若函数axaaxxxf.)6()41(1)1(2131)(23的取值范围实数上是增函数,求,上是减函数,在区间,在区间若函数axaaxxxf例2.例2.湖南省长沙市一中卫星远程学校例题讲解例题讲解题型二:证明不等式题型二:证明不等式湖南省长沙市一中卫星远程学校例题讲解例题讲解例1.已知x>1,求证:x>ln(1+x).例1.已知x>1,求证:x>ln(1+x).题型二:证明不等式题型二:证明不等式湖南省长沙市一中卫星远程学校例题讲解例题讲解例1.已知x>1,求证:x>ln(1+x).例1.已知x>1,求证:x>ln(1+x).题型二:证明不等式题型二:证明不等式例2.已知x>0,求证:1+2x>例2.已知x>0,求证:1+2x>.2xe.2xe湖南省长沙市一中卫星远程学校例题讲解例题讲解题型二:证明不等式题型二:证明不等式湖南省长沙市一中卫星远程学校例题讲解例题讲解题型二:证明不等式题型二:证明不等式例3.例3..tansin)20(xxxx,求证:,已知.tansin)20(xxxx,求证:,已知湖南省长沙市一中卫星远程学校例题讲解例题讲解题型二:证明不等式题型二:证明不等式例3.例3..tansin)20(xxxx,求证:,已知.tansin)20(xxxx,求证:,已知.211821,02xxxxx证明不等式已知.211821,02xxxxx证明不等式已知练习:练习:湖南省长沙市一中卫星远程学校小结小结若证明f(x)>g(x),x(∈a,b)可以等价转换为证明f(x)-g(x)>0,如果(f(x)-g(x))'>0,说明函数f(x)-g(x)在(a,b)上是增函数,如果f(a)-g(a)≥0,由增函数的定义可知,当x∈(a,b)时,f(x)-g(x)>0,即f(x)>g(x).若证明f(x)>g(x),x(∈a,b)可以等价转换为证明f(x)-g(x)>0,如果(f(x)-g(x))'>0,说明函数f(x)-g(x)在(a,b)上是增函数,如果f(a)-g(a)≥0,由增函数的定义可知,当x∈(a,b)时,f(x)-g(x)>0,即f(x)>g(x).湖南省长沙市一中卫星远程学校例题讲解例题讲解题型三:有关方程根的问题题型三:有关方程根的问题湖南省长沙市一中卫星远程学校例题讲解例题讲解题型三:有关方程根的问题题型三:有关方程根的问题例1.例1..00sin21:xxx只有一个根方程求证.00sin21:xxx只有一个根方程求证湖南省长沙市一中卫星远程...