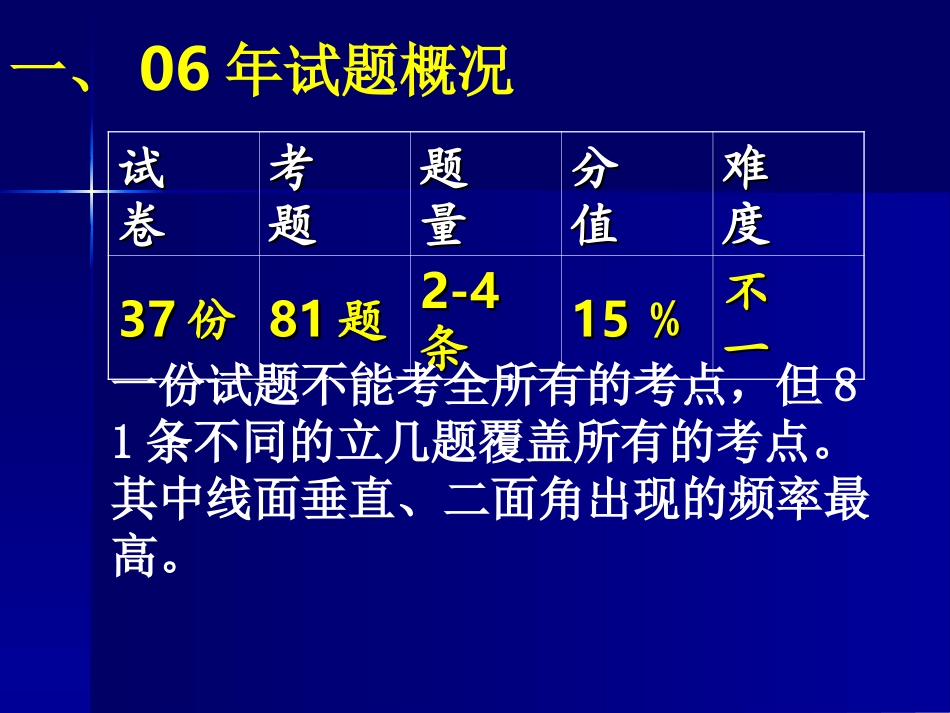
透视06高考把握07复习——立体几何一、06年试题概况试试卷卷考考题题题题量量分分值值难难度度3737份份8181题题2-42-4条条1515%%不不一一一份试题不能考全所有的考点,但81条不同的立几题覆盖所有的考点。其中线面垂直、二面角出现的频率最高。二、06年试题分析1、一种考法考查基础知识的同时,注重考查能力【说明】本题考查正四面体的性质、线段在平面内的射影;空间想象能力、等价转化能力【说明】本题考查正四面体的性质、线段在平面内的射影;空间想象能力、等价转化能力[06浙江14]正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是_____ElCDEC1E1D1[06浙江14]多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面内,其余顶点在的同侧,正方体上与顶点A相邻的三个顶点到的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可是:①3;②4;③5;④6;⑤7以上结论正确的为_______________。(写出所有正确结论的编号)ABCDA1B1C1D1分析:在解析几何中”已知平行四边形的三个顶点坐标,求第四个点坐标”平移到空间就是”已知平行四边形的三个顶点到一个平面的距离,求第四个点到这个平面的距离”124利用相等向量在直线上的射影长相等,推得在空间互相平行且长度相等的线段在同一直线或互相平行的直线上的射影长相等【说明】本题考查正方体的性质、点面距离、空间想象能力和迁移能力【说明】本题考查正方体的性质、点面距离、空间想象能力和迁移能力2、两类题型定性平行、垂直存在性唯一性任意性[06天津(理)6]设m、n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是A、m⊥α,n⊂β,m⊥nα⇒⊥βB、αβ∥,m⊥α,n∥β⇒m⊥nC、α⊥β,m⊥α,n∥β⇒m⊥nD、α⊥β,α∩β=m,m⊥n⇒n⊥β【说明】本题考查线线、线面、面面的平行垂直关系【说明】本题考查线线、线面、面面的平行垂直关系αnmαmnβαnmβαβmn[06湖南(理)3]过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有A、4条B、6条C、8条D、12条【说明】线∥线线∥面面∥面面∥线⇒⇒⇒【说明】线∥线线∥面面∥面面∥线⇒⇒⇒分析:同侧的四个中点M、N、E、F构成的矩形与对角面平行,它们任两点的连线都与对角面平行,共6条,6×2=12条AA1与其它中点连线与对角面不平行ABCDA1D1C1B1EFNMH[06重庆(文)4]若P是平面α外一点,则下列命题正确的是(A)过P只能作一条直线与平面α相交(B)过P可作无数条直线与平面α垂直(C)过P只能作一条直线与平面α平行(D)过P可作无数条直线与平面α平行【说明】过一点作已知平面的垂线有且只有一条(唯一性)过平面外一点可作无数直线与已知平面平行(存在性)[06重庆(文)4]对于任意的直线l与平面α,在平面α内必有直线m,使m与l()(A)平行(B)相交(C)垂直(D)互为异面直线【说明】本题考查线线关系、线面关系、分类思想、任意性问题分析:A反例:l⊥αB反例:l∥αD反例:l⊂αC:①lα∥②斜交③垂直④l⊂α定量角距离面积与体积异面直线所成角线面角二面角点面距离球面距离[06上海(文)19]在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.1)求异面直线B1C1与AC所成角说明:图中现成的角∠ACB=45°ACBB1C1A1[06福建(文)19]如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=(Ⅰ)求证:平面BCD;(Ⅱ)求异面直线AB与CD所成角的大小;(Ⅲ)略2CADBOEF【说明】1.过空间特殊点E引平行线得所求角2.过异面直线中一条线引另一直线的平行线得所求角M【说明】异面直线所成角1)图中有现成角2)过其中一条直线上的点作另一条直线的平行线3)过不在已知直线上的特殊点分别引这两条直线的平行线【说明】异面直线所成角1)图中有现成角2)过其中一条直线上的点作另一条直线的平行线3)过不在已知直线上的特殊点分别引这两条直线的平行线[06浙江(理)17]如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.(Ⅰ)求证:PB⊥...