福建省高一数学向量的加法课件 人教版 课件VIP免费

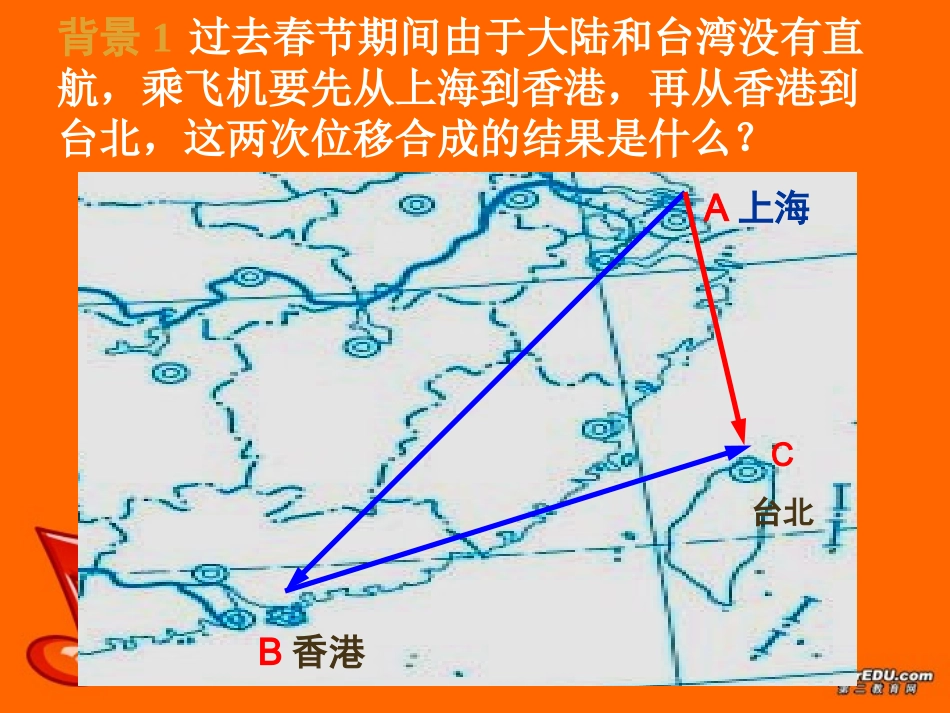
复习提问：1、什么叫向量？2、方向相同或相反的非零向量叫3、什么叫相等向量？既有大小又有方向的量叫向量长度相等且方向相同的向量叫相等向量。平行向量或共线向量背景1过去春节期间由于大陆和台湾没有直航，乘飞机要先从上海到香港，再从香港到台北，这两次位移合成的结果是什么？香港上海A上海B香港C台北背景背景22图a表示橡皮条在两个力的作用下沿GO伸长了EO图b表示橡皮条在力F的作用下沿GO伸长了相同的长度EOF与F1、F2之间的关系如何？探究1如何定义两个向量的和？baOaaaaabbbbbbb这种作法叫做三角形法则BbaAO在平面内任取一点作法1bAB,aOA作2baOB3则向量a+b1、向量的加法的三角形法则归纳一下三角形法则的特点abba2.向量的加法的平行四边形法则baAaaaabbbBbaDaCba+b作法:(1)在平面取一点A(2)以点A为起点以向量a、b为邻边作平行四边形ABCD.即AD＝BC＝a,AB=DC=b（3）则以点A为起点的对角线AC＝a+b这种作法叫做平行四边形法则归纳一下平行四边形形法则的特点bDbCaa+b探究2：求和时用三角形法则与平行四边形法则一样吗？比较一下两种法则BaAbCa+bBaA特点：（通过平移）首尾相接特点：（通过平移）起点相同不同法则，效果相同abba（1）（2）abbaab练习1.如图,已知用向量加法的三角形法则作出baba错啦OABOBACOB＝a+b即为所求CA＝a+b即为所求a（1）abbaabba（2）ab练习2.如图,已知用向量加法的平行四边形法则作出baaaaabbbbaaabbbbOOAAOA＝a+b即为所求OA＝a+b即为所求abba探究3特例：abABC方向相同C方向相反baACbaACaa00a:注a在这种情况下，可以使用平行四边形法则吗？ABb(a+b)+c=a+(b+c)向量的多边形法则:多个向量相加,通过向量的平移将它们顺序“首尾相接",则以第一个向量的起点为起点,以最后一个向量的终点为终点的向量,即为这多个向量的和向量.OA+AB+BC=_______OC探究探究44：：求求22个以上向量的和向量个以上向量的和向量O(a+b)+c=_____+____=______OBOCa+(b+c)=OA+_____=______ACcaAbBcCOCBC首尾相接首尾连nnnnnAAAAAAAAAA01122110一般的3、向量加法的运算律abba:1交换律)()cb(ac)ba(:2结合律)(有了这两个法则，多个向量的加法就可以按照任意的次序和组合来进行了abbaabAB。就是船实际航行的速度，则为邻边作平行四边形、表示水流的速度，以驶的速度表示船向垂直于对岸行解：如图，设ACABCDABADABAD432222||||||||||BCABACBCABABCRt，中△在流速间的夹角表示）的大小和方向。（用与，求船实际航行速度流速为方向行驶，同时河水的的速度向垂直于对岸的点出发以如图，一艘船从hkmhkmA232ABDC603CABCABtan∵答：船实际航行的速度为大小为4km／h，方向与流速间的夹角为600应用举例练习3根据图示填空CabcdefgABDEedc)4(dba)3(dc)2(ba)1(cffg练习4:试用向量方法证明：对角线互相平分的四边形是平行四边形。已知四边形ABCD，对角线AC与BD交于O，AO=OC，DO=OB。求证四边形ABCD是平行四边形ABCDO证如图，由向量加法法则，有OBAOABOBOCAODO，又已知OCDODC为平行四边形平行且相等与即ABCDDCABDCAB小结1向量加法法则：三角形法则平行四边形法则ababbaba2运算性质:aaacbacbaabba00)()(ab作业课本P104习题5.21、2、3、4