高考数学一轮复习 8.7 立体几何中的向量方法精品课件 新人教A版 课件VIP免费

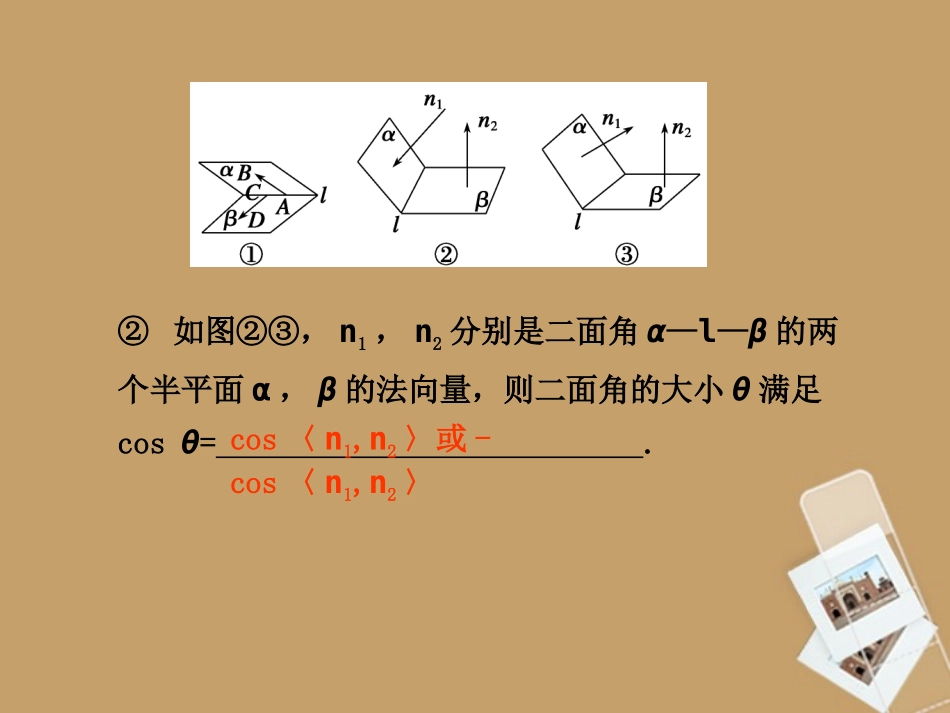
§8.7立体几何中的向量方法要点梳理1.直线的方向向量与平面的法向量的确定（1）直线的方向向量：在直线上任取一向量作为它的方向向量.（2）平面的法向量可利用方程组求出：设a,b是平面α内两不共线向量，n为平面α的法向量，则求法向量的方程组为非零.00bnan基础知识自主学习2.空间向量与空间角的关系(1)设异面直线l1,l2的方向向量分别为m1,m2，则l1与l2所成的角θ满足.(2)设直线l的方向向量和平面α的法向量分别为m,n，则直线l与平面α所成角θ满足.(3)求二面角的大小①如图①，AB、CD是二面角α—l—β的两个面内与棱l垂直的直线,则二面角的大小θ=.cosθ=|cos〈m1,m2〉|sinθ=|cos〈m,n〉|CDAB,②如图②③，n1，n2分别是二面角α—l—β的两个半平面α，β的法向量，则二面角的大小θ满足cosθ=.cos〈n1,n2〉或-cos〈n1,n2〉3.点面距的求法如图,设AB为平面α的一条斜线段,n为平面α的法向量,则B到平面α的距离d=.||||nnAB基础自测1.若直线l1,l2的方向向量分别为a=(2,4,-4),b=(-6,9,6)，则()A.l1∥l2B.l1⊥l2C.l1与l2相交但不垂直D.以上均不正确解析 a·b=-12+36-24=0，∴a⊥b，∴l1⊥l2.B2.已知平面α内有一个点M（1，-1，2），平面α的一个法向量是n=（6，-3，6），则下列点P中在平面α内的是()A.P（2，3，3）B.P（-2，0，1）C.P（-4，4，0）D.P（3，-3，4）解析 n=（6，-3，6）是平面α的法向量，∴n⊥，在选项A中，=（1，4，1），∴n·=0.AMPMPMP3.已知两平面的法向量分别为m=（0，1，0），n=（0，1，1）,则两平面所成的二面角为()A.45°B.135°C.45°或135°D.90°解析即〈m,n〉=45°，其补角为135°.∴两平面所成二面角为45°或135°.,22211||||,cosnmnmnmC4.如图所示，在空间直角坐标系中，有一棱长为a的正方体ABCO—A′B′C′D′，A′C的中点E与AB的中点F的距离为()A.B.C.aD.解析由图易知A（a,0,0）,B（a,a,0）,C（0，a，0），A′(a,0,a).a2a22a21.2244)20()22()2(||).2,2,2(),0,2,(22222aaaaaaaaEFaaaEaaFB5.已知a=(1,1,1),b=(0,2,-1),c=ma+nb+(4,-4,1).若c与a及b都垂直，则m,n的值分别为()A.-1,2B.1,-2C.1,2D.-1,-2解析由已知得c=(m+4,m+2n-4,m-n+1),故a·c=3m+n+1=0，b·c=m+5n-9=0..2,1nm解得A题型一利用空间向量证明平行与垂直如图所示，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明：(1)AE⊥CD;(2)PD⊥平面ABE.【例1】题型分类深度剖析思维启迪（1）建立空间直角坐标系确定的坐标CD、AE计算CDAEAE⊥CD（2）求面ABE的法向量n判断满足=kn(k∈R）PD⊥平面ABEPD或确定坐标AE、AB、PD计算AEPDABPD,PD⊥AEPD⊥ABPD⊥平面ABE证明AB、AD、AP两两垂直，建立如图所示的空间直角坐标系，设PA=AB=BC=1，则P（0，0，1）.(1) ∠ABC=60°，∴△ABC为正三角形.),0,332,0(,332,0,),0,,0().21,43,41(),0,23,21(DyCDACCDACyDEC则即得由设),21,43,41().0,63,21(AECD又.,,043634121CDAECDAECDAE即(2)方法一).1,332,0(),1,0,0(PDP.,,,0),0,0,1(.,,0)1(2133243AEBPDAAEABABPDABPDABAEPDAEPDPDAE平面又即又方法二),21,43,41(),0,0,1(AEAB.,,//.33),1,332,0().3,2,0(,3,2,02143410),,,(ABEPDABEPDPDPDPDzyzyxxzyxABE平面即平面显然则令则的一个法向量为设平面nnnn证明线面平行和垂直问题，可以用几何法，也可以用向量法.用向量法的关键在于构造向量，再用共线向量定理或共面向量定理及两向量垂直的判定定理.若能建立空间直角坐标系，其证法较为灵活方便.探究提高知能迁移1如图所示,平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点.求证：PB∥平面EFG.证明 平面PAD⊥平面ABCD且ABCD为正方形,∴AB、AP、AD两两垂直，以A为坐标原点，建立如图所示的空间直角坐标系A—xyz，则A(0,0,0)、B(2,0,0)、C(2,2,0)、D(0,2,0)、P(0,0,2)、E(0,0,1)、F(0,1,1)、G(1,2,0).),1,1...