高一数学一元二次不等式的解法 苏教版 课件VIP免费

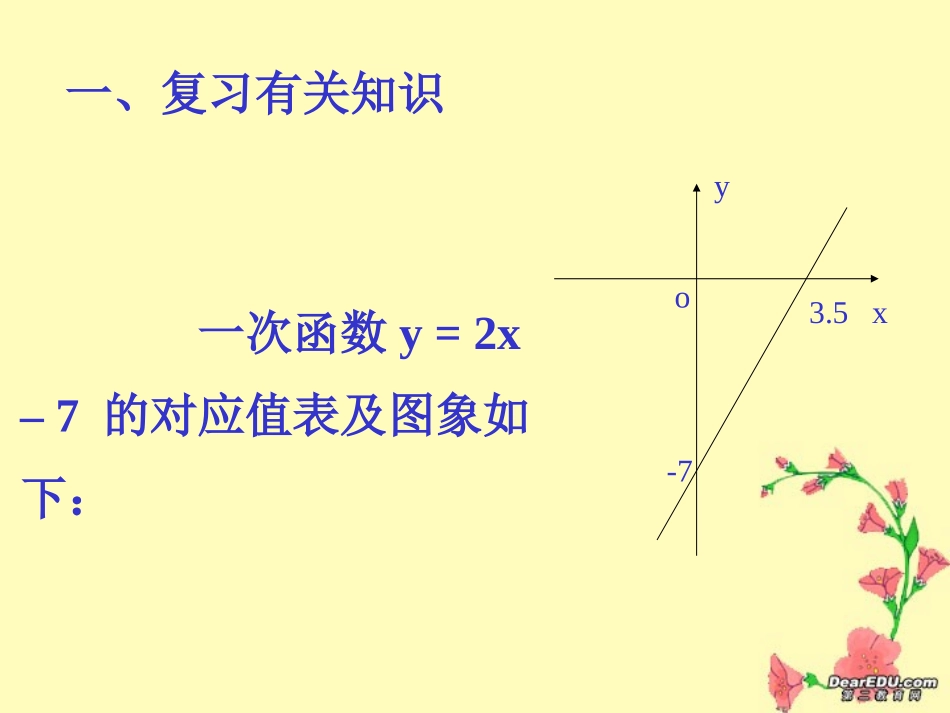
1.5一元二次不等式的解法（1）在初中，我们学过一元一次不等式的解法、一元二次方程的解法以及二次函数的有关知识，那么，一元一次方程、一元一次不等式与一次函数有什么关系呢？类似地，一元二次方程、一元二次不等式与二次函数之间又有怎样的关系呢？一、复习有关知识3.5xyo-7一次函数y=2x–7的对应值表及图象如下：x22.533.544.55y-3-2-10123填空：当x=3.5时，y=____,得2x–7____0;当x<3.5时，y____0,得2x–7____0;当x>3.5时，y____0,得2x–7____0.0=<<>>结论：直线与x轴交点的横坐标，就是对应的一元一次方程的根，再结合直线的位置，就可以确定对应的一元一次不等式的解集。那么，对一元二次方程、一元二次不等式与二次函数的关系怎样处理呢？二、探索新知1一元二次不等式的解法先看二次函数y=x2–x–6的图象：x-3-2-101234y60-4-6-6-406当x=-2或3时，y=x2–x–6=0;当x<-2或x>3时，y=x2–x–6>0;当-20y<0yy=x2–x–6归纳可知，对于一元二次方程ax2+bx+c=0(a>0),设=b2–4ac,它的解按照>0,=0,<0分为三种情况。相应地，抛物线y=ax2+bx+c(a>0)与x轴的相关位置也分为三种情况：(1)>0的情况：x1ox2xyax2+bx+c=0(a>0)的根x10(a>0)的解集{x|xx2};ax2+bx+c<0(a>0)的解集{x|x10)的根x1=x2;ax2+bx+c>0(a>0)的解集{x|xx1};ax2+bx+c<0(a>0)的解集为Ø。(3)<0的情况：oxyax2+bx+c=0(a>0)无实根;ax2+bx+c>0(a>0)的解集为R;ax2+bx+c<0(a>0)的解集为Ø。？思考：a<0时，情况又如何？该怎样处理？以上结论可以用以下口诀记忆：开口向上大于零，两根之外；开口向上小于零，两根之间。说明：如果不等式有等号，在答案中加上即可。例1解不等式：(1)x2–x–2<0;(2)4x2–4x+1>0;(3)-x2+2x–30.提示求解步骤：求根—看图—写解集练习：P.76.1~42201,3bxxab2例已知不等式ax的解１为：－求、的值。２1例３当a>0时，解不等式（x-a）(x-)<0.a小结：1一元二次不等式的解法、解集。2将一元二次函数、一元二次方程和一元二次不等式联系起来处理，效果会更好。作业:习题p811~4课时详解P.51.