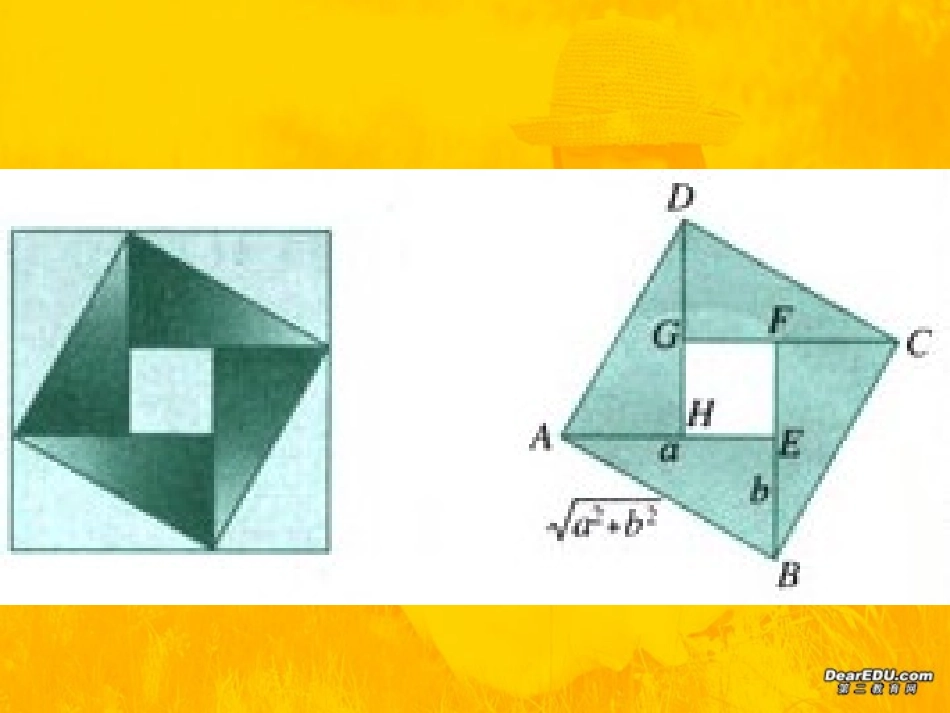
如图是在北京召开的第24界国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。你能在这个图案中找出一些相等关系或不等关系吗?一般的,如果22,R,2("")abababab那么当且仅当时取号1.重要不等式如果a>0,b>0,那么abba22.均值定理ⅰ))))baba,2为)))))))baab,为))))))))))此定理又可叙述为:两个正数的算术平均数不小于它们的几何平均数.ⅱ)abbaabba2222和成立的条件是不同的:前者只要求a,b都是实数,而后者要求a,b都是正数.ⅲ“”)当且仅当的含义是充要条件.在右图中,AB是圆的直径,点C是AB上的一点,AC=a,BC=b。过点C作垂直于AB的弦DE,连接AD、BD。你能利用这个图形得出基本不等式的几何解释吗?abba23.均值定理的几何意义;2P例1已知x,y都是正数,求证:(1)如果积xy是定值P,那么当x=y时,和x+y有最小值.412S(2)如果和x+y是定值S,那么当x=y时,积xy有最大值说明:此例题反映的是利用均值定理求最值的方法,但应注意三个条件:ⅰ)函数式中各项必须都是正数;ⅱ)函数式中含变数的各项的和或积必须是常数;ⅲ)等号成立条件必须存在.24624mm例1已知m>0,求证24m6m[思维切入]因为m>0,所以可把和分别看作基本不等式中。的a和b,直接利用基本不等式()()4abcdacbdabcd3.随堂练习1[思维拓展1]已知a,b,c,d都是正数,求证[思维拓展2].22222()()()abcdacbd求证:473aa例2求证:44(3)333aaaa.[思维切入]由于不等式左边含有字母a,右边无字母,直接使用基本不等式,无法约掉字母a,而左边.这样变形后,在用基本不等式即可得证.281xy[思维拓展2]若x>0,y>0,且,求xy的最小值.9()45fxxx随堂练习2[思维拓展1]求(x>5)的最小值.