高考数学 第六节 对数与对数函数(一)课件 新人教版 课件VIP免费

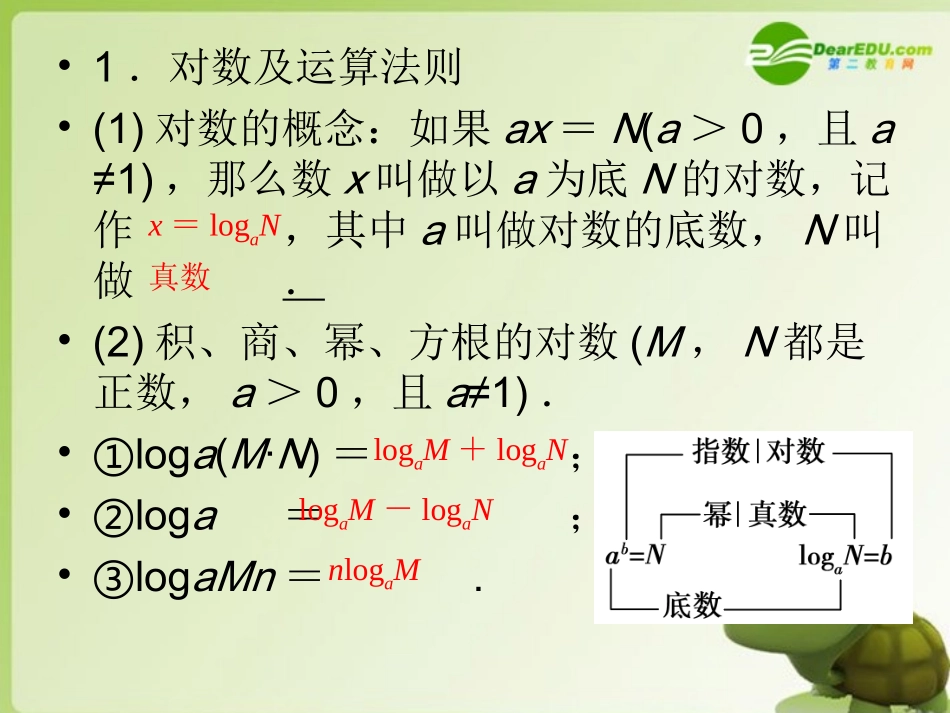
•1．对数及运算法则•(1)对数的概念：如果ax＝N(a＞0，且a≠1)，那么数x叫做以a为底N的对数，记作，其中a叫做对数的底数，N叫做．•(2)积、商、幂、方根的对数(M，N都是正数，a＞0，且a≠1)．•①loga(M·N)＝；•②loga＝；•③logaMn＝.x＝logaN真数logaM＋logaNlogaM－logaNnlogaM•（3）对数恒等式及换底公式•①••②•③•④log(0,0,0)aNaNaaN且loglog(0,1,0,0,1)logbabNNaaNbba1log(0,1,0,1)logabbaabbalog(0,1)loglog(0,1,0)mnanaaanaanNNaaNm•2．对数函数及性质•(1)一般地，我们把函数y＝(a＞0，且a≠1)叫做对数函数．•(2)对数函数的图象和性质xalog图象对数函数性质x＞0，y∈(－∞，＋∞)当x＝1时，y＝0在(0，＋∞)上是增函数当x＞1时，y∈；当0＜x＜1时，y∈在(0，＋∞)上是减函数当x＞1时，y∈；当0＜x＜1时，y∈(0，＋∞)(－∞，0)(－∞，0)(0，＋∞)•3.指数函数与对数函数的区别与联系•指数函数y＝(a＞0，且a≠1)与•互为反函数，它们的图象关于对称．•xa对数函数y＝logax(a＞0，且a≠1)直线y＝x•如何确定图中各函数的底数a，b，c，d与1的大小关系？•提示作一直线y＝1，该直线与四个函数图象交点的横坐标即为它们相应的底数．∴0＜c＜d＜1＜a＜b.基础练习•①求的值•②已知，求x.•③已知，求的值。•④的值。4log84327logxnmaa3log,2lognma25lg24lg答案：①32②81x③12④2答案：D•A．x＞y＞zB．z＞y＞x•C．y＞x＞zD．z＞x＞y答案C答案A这类问题主要用到对数的恒等式和对数的运算法则．务必注意化简前后的等价性．同时还要注意对数式与指数式之间的相通性．计算下列各题：•思维提示(1)直接运用对数运算法则化简运算；•(2)先利用幂的运算把真数化简，然后再运用对数运算法则；•(3)先对其式进行一般代数运算的化简，然后利用同底对数运算．课堂练习一•求值：①②2)2(lg20lg5lg8lg3225lg)3log2)(log2log2log8493（答案：①3②45归纳总结：•一：知识点•对数的概念•对数的运算法则•对数的运算性质•二，对数运算要注意的问题•在对数式的求值或化简中遵循着“大化小”“繁化简”的原则。布置作业：•题组一对数与对数的运算•祝各位身心健康，学习愉快•谢谢！•再见！