高三数学数形结合的思想方法课件VIP免费

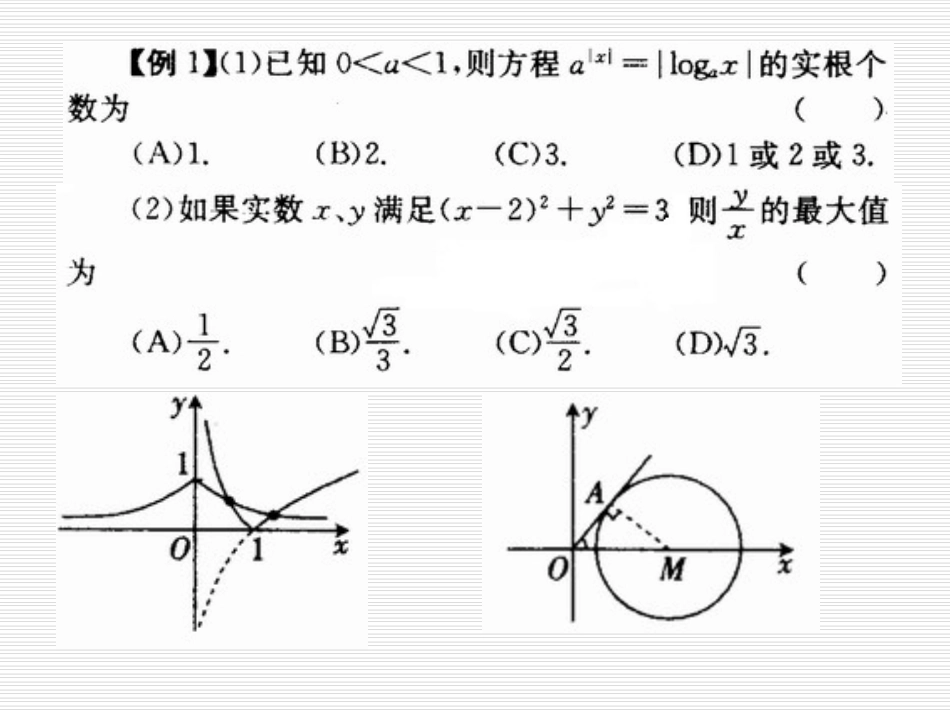
数形结合的思想方法授课人：张敏数缺形时少直观，形少数时难入微；数形结合百般好，隔裂分家万事非。——华罗庚例1（1）已知0＜a＜1，则方程a|x|=|logax|的实根个数为（A）1（B）2（C）3（D）1或2或3（2）如果实数x、y满足(x-2)2+y2=3，则xy的最大值为（A）21（B）33（C）23（D）3（3）若关于x的方程x2+2kx+3k=0的两根都在-1和3之间，则k的取值范围为________________。（4）不等式2x＞x的解集为___________。（5）若集合M={（x,y）|)0(sin3cos3yx}，集合N={（x,y）|y=x+b}，且NMф，则b的取值范围为______________。xy21332332x)0(sin3cos3yxNM学生自测：。。xy-3-3-3知识整合实现数形结合，常与以下内容有关实数与数轴上的点的对应关系函数与图象的对应关系曲线与方程的对应关系概念本身的几何意义所给等式的结构有明显几何意义xxyy1xoye1/e