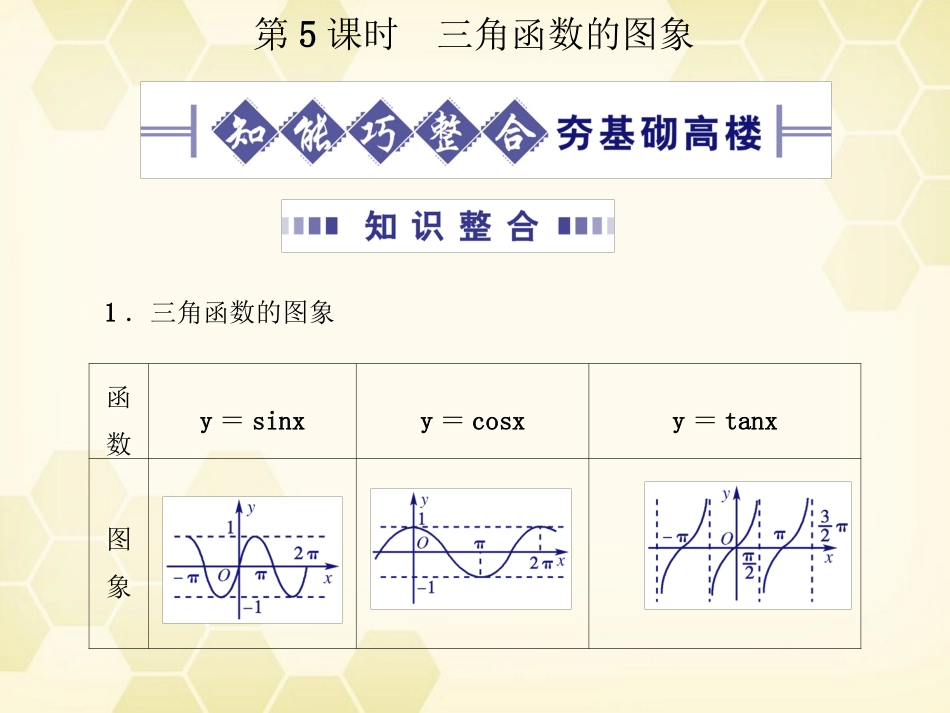
第5课时三角函数的图象函数y=sinxy=cosxy=tanx图象1.三角函数的图象作函数y=Asin(ωx+φ)的图象的方法常用的有五点作图法和图象变换法.五点作图法是最基本的作图方法,一般步骤是:(1)将函数整理成y=Asin(ωx+φ)的形式;(2)列表,令z=ωx+φ,分别令z=0,,π,,2π,求出相应的x值x1,x2,x3,x4,x5,及相应的y值0,A,0,-A,0,列成表格;(3)描点,在坐标系中作出五个点(x1,0),(x2,A),(x3,0),(x4,-A),(x5,0),即函数y=Asin(ωx+φ)的图象的一个周期上的五个点;(4)连线,用平滑曲线顺次连接起五个点,再向两端延伸即可得到函数在整个定义域上的图象.[注意]“”五点法作图的关键在于抓好y=Asin(ωx+φ)的五个特征点上的最值点和三个平衡位置点(即零点),对“于零点还要从图象的升降情况判断其为第”“”一零点还是第二零点.1.平移变换(1)沿x“”轴平移,按左加右减法则;(2)沿y“”轴平移,按上加下减法则.2.伸缩变换(1)沿x轴伸缩时,横坐标x伸长(0<ω<1)或缩短(ω>1)为原来的倍(纵坐标y不变);(2)沿y轴伸缩时,纵坐标y伸长(A>1)或缩短(0