高考数学第一轮总复习8.5直线与圆锥曲线的位置关系(第2课时)课件 文 (广西专版) 课件VIP免费

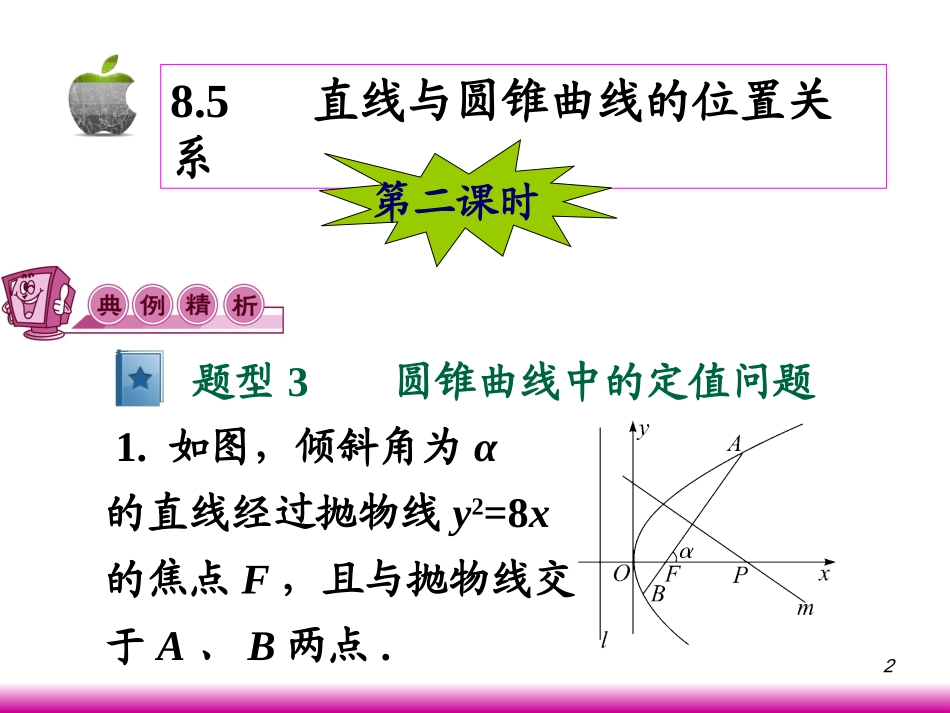
1第八章圆锥曲线方程28.5直线与圆锥曲线的位置关系第二课时题型3圆锥曲线中的定值问题1.如图，倾斜角为α的直线经过抛物线y2=8x的焦点F，且与抛物线交于A、B两点.3(1)求抛物线的焦点F的坐标及准线l的方程；(2)若α为锐角，作线段AB的垂直平分线m交x轴于点P，证明|FP|-|FP|cos2α为定值，并求此定值.解：(1)设抛物线的标准方程为y2=2px，则2p=8，从而p=4.因此焦点F(,0)的坐标为(2，0).又准线方程的一般式为x=-.从而所求准线l的方程为x=-2.2p2p4(2)解法1:如图,作AC⊥l,BD⊥l,垂足分别为C、D，则由抛物线的定义知|FA|=|AC|,|FB|=|BD|.记A、B的横坐标分别为xA、xB，则解得||||2||cos||cos4,22ApFAACxppFAFA4||.1-cosFA5类似地,有|FB|=4-|FB|cosα,解得记直线m与AB的交点为E，则所以故为定值.4||.1cosFB2||||||||-||||-211444cos(||-||)(-).221-cos1cossinFAFBFEFAAEFAFAFB2||4||.cossinFEFP222442sin||-||cos2(1-cos2)8sinsinFPFP6解法2：设A(xA,yA)，B(xB,yB)，直线AB的斜率为k=tanα，则直线AB的方程为y=k(x-2).将上式代入y2=8x,得k2x2-4(k2+2)x+4k2=0，故记直线m与AB的交点为E(xE,yE)，则故直线m的方程为224(2).ABkxxk222(2)4,(-2),2ABEEExxkxykxkk224124--(-).kyxkkk7令y=0,得P的横坐标故从而为定值.点评：探求有关定值问题，一是可以转化为求值问题来解，二是可以考虑特殊情况时的解.22244,Pkxk2224(1)4||-2.sinPkFPxk222442sin||-||cos2(1-cos2)8sinsinFPFP8如图,已知点F(1,0),直线l:x=-1，P为平面上的动点，过P作直线l的垂线,垂足为Q,且(1)求动点P的轨迹C的方程；(2)过点F的直线交轨迹C于A、B两点，交直线l于点M,已知试推断λ1+λ2是否为定值，并说明理由.拓展练习拓展练习.QPQFFPFQ�12,,MAAFMBBF�9解:(1)设点P(x,y),则Q(－1，y).由得(x+1,0)·(2,-y)=(x-1,y)·(-2,y),化简y2=4x.所以动点P的轨迹C的方程为y2=4x.(2)设直线AB的方程为x=my+1(m≠0).设A(x1，y1)，B(x2，y2)，又M(-1，-).,QPQFFPFQ�2m10联立方程组消去x得y2=4my+4，则Δ=(-4m)2+16>0,故由得整理得所以为定值.24,1yxxmy12124.-4yymyy12,,MAAFMBBF�11122222-,-,yyyymm121222-1-,-1-,mymy121212122112-2-()-2-24-2-0,-4yymyymyymm112.已知直线x-2y+2=0经过椭圆C:(a>b>0)的左顶点A和上顶点D，椭圆C的右顶点为B，点S和椭圆C上位于x轴上方的动点，直线AS,BS与直线l:x=分别交于M,N两点.(1)求椭圆的方程；(2)求线段MN的长度的最小值；题型4圆锥曲线中的最值与范围问题10322221xyab12(3)当线段MN的长度最小时，在椭圆C上是否存在这样的点T，使得△TSB的面积为？若存在，确定点T的个数；若不存在，说明理由.解：(1)由已知得，椭圆C的左顶点为A(-2,0)，上顶点为D(0,1),所以a=2,b=1,故椭圆C的方程为(2)直线AS的斜率k显然存在，且k>0，故可设直线AS的方程为y=k(x+2),从而15221.4xy1016(,).33kM13由得(1+4k2)x2+16k2x+16k2-4=0,设S(x1,y1),则得从而即又B(2,0)，故直线BS的方程为由得所以故22(2),14ykxxy21216-4(-2),14kxk2122-8,14kxk124,14kyk2222-84(,),1414kkSkk1-(-2).4yxk1-(-2)4,103yxkx103,1-3xyk101(,-),33Nk161||||.33kMNk14又k>0，所以当且仅当即时等号成立.所以时，线段MN的长度取最小值.(3)由(2)可知，当MN取最小值时，,此时BS的方程为x+y-2=0,所以要使椭圆C上存在点T，使得△TSB的面积等于，只须T到直线BS的距离等于，1611618||2,33333kkMNkk161,33kk14k14k8314k64(,),55S42||.5BS152415所以T在平行于BS且与BS距离等于的直线l'上.设直线l':x+y+t=0,则由解得或①当时，由得5x2-12x+5=0.由于Δ=44>0,故直线l'与椭圆C有两个不同的交点;②当时，由得5x2-20x+21=0.24|2|2,42t3-2t5-.2t3-2t2214,3-02xyxy5-.2t2214,5-02xyxy...