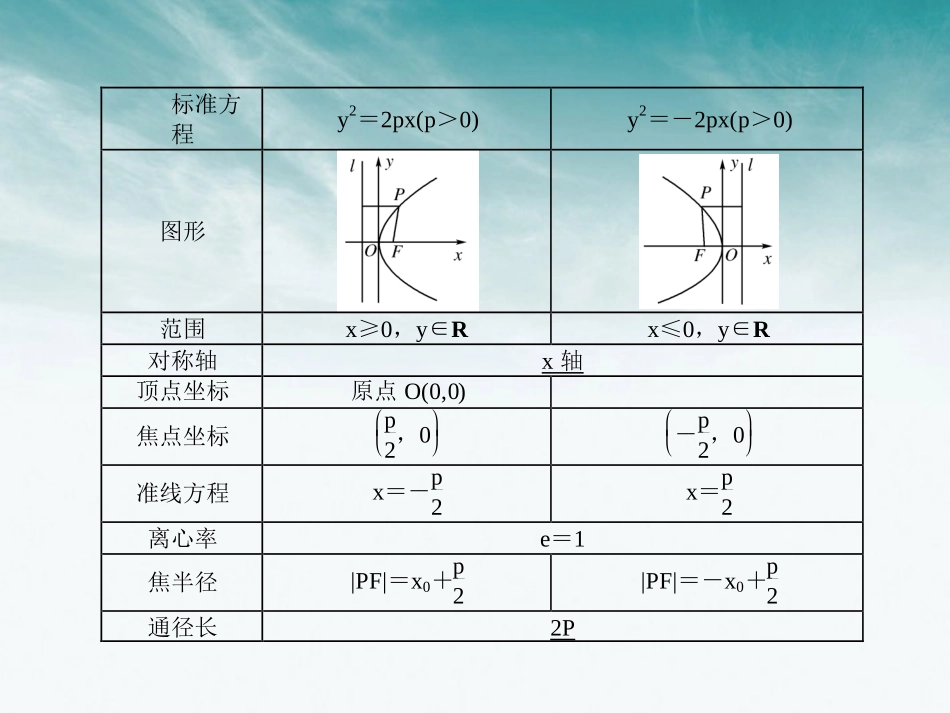
第二节抛物线1.拋物线定义平面内与一个定点F和一条定直线l的距离的轨迹叫做拋物线,点F叫做拋物线的焦点,直线l叫做拋物线的,定点F不在定直线l上.当定点F在定直线l上时,动点的轨迹是什么图形?【提示】当定点F在定直线l上时,动点的轨迹是过点F且与直线l垂直的直线.相等的点准线标准方程y2=2px(p>0)y2=-2px(p>0)图形范围x≥0,y∈Rx≤0,y∈R对称轴x轴顶点坐标原点O(0,0)焦点坐标p2,0-p2,0准线方程x=-p2x=p2离心率e=1焦半径|PF|=x0+p2|PF|=-x0+p2通径长2P标准方程x2=2py(p>0)x2=-2py(p>0)图形范围y≥0,x∈Ry≤0,x∈R对称轴y轴顶点坐标原点O(0,0)焦点坐标0,p20,-p2准线方程y=-p2y=p2离心率e=1焦半径|PF|=y0+p2|PF|=-y0+p2通径长2P其中p表示焦点到准线的距离,其恒为正数.(1)p的几何意义:p是焦点到准线的距离,故p恒为正数.(2)拋物线标准方程的形式特点①形式为y2=±2px或x2=±2py;②一次项的变量与焦点所在的坐标轴的名称相同,一次项系数的符号决定拋物线的开口方向,即“对称轴看一次项,符号决定开口方向”;③焦点的非零坐标是一次项系数的14.焦点在x轴上的拋物线的标准方程可统一写成y2=ax(a≠0);焦点在y轴上的拋物线的标准方程可统一写成x2=ay(a≠0).1.若拋物线y2=2px的焦点与椭圆x26+y22=1的右焦点重合,则p的值为()A.-2B.2C.-4D.4【解析】椭圆x26+y22=1的右焦点为(2,0),所以拋物线y2=2px的焦点为(2,0),则p=4.【答案】D2.顶点在原点,关于坐标轴对称,且过点(2,-3)的抛物线方程是()A.y2=92xB.x2=-43yC.y2=92x或x2=-43yD.以上都不正确【解析】分焦点在x轴和y轴上求解.选C.【答案】C3.在拋物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为()A.12B.1C.2D.4【解析】由拋物线定义可知:p2+4=5,∴p=2.【答案】C4.设抛物线的顶点坐标为(2,0),准线方程为x=-1,则它的焦点坐标为________.【解析】将抛物线向左平移2个单位长度将准线方程变为x=-3,故新抛物线方程为y2=12x.它的焦点坐标为(3,0),故原抛物线焦点坐标为(5,0).【答案】(5,0)5.过抛物线y2=4x的焦点F作垂直于x轴的直线,交抛物线于A、B两点.则以F为圆心、AB为直径的圆方程是________.【解析】由y2=4x得F(1,0),令x=1,代入y2=4x得:y=±2,∴|AB|=4,故所求圆的方程为(x-1)2+y2=4.【答案】(x-1)2+y2=4求下列各拋物线的标准方程:(1)顶点在坐标原点,对称轴为坐标轴,且经过点M(-2,-4);(2)顶点在坐标原点,焦点在y轴上,拋物线上一点Q(m,-3)到焦点的距离等于5.【思路点拨】确定拋物线方程的那种形式,本利用待定系数法求参数p.【解析】(1)设拋物线为y2=mx或x2=ny,则(-4)2=m(-2)⇒m=-8.或(-2)2=n(-4)⇒n=-1.∴所求的拋物线方程为y2=-8x或x2=-y.(2)依题意,拋物线开口向下,故设其方程为x2=-2py.则准线方程为y=p2,又设焦点为F,则|QF|=p2-yQ,即p2-(-3)=5⇒p=4.故拋物线方程为x2=-8y.已知拋物线y2=2x的焦点是F,点P是拋物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标.重视定义在解题中的应有,灵活地进行拋物线上的点到焦点的距离与到准线距离的等价转化,是解决拋物线焦点弦有关问题的重要途径.1.过拋物线y2=2px(p>0)的焦点F任作一条直线m,交此拋物线于P1、P2两点,求证以P1、P2为直径的圆和这条拋物线的准线相切.【证明】如图所示,设P1、P2的中点为P0,过P1、P2、P0分别向准线l引垂线,垂足分别为Q1、Q2、Q0,根据拋物线的定义得:|P1F|=|P1Q1|,|P2F|=|P2Q2|,∴|P1P2|=|P1F|+|P2F|=|P1Q1|+|P2Q2|. P1Q1P0Q0P2Q2∥∥,|P1P0|=|P0P2|,A、B是拋物线y2=2px(p>0)上的两点,且OAOB.⊥(1)求A、B两点的横坐标之积和纵坐标之积;(2)求证:直线AB过定点;(3)求△AOB面积的最小值.【解析】(1)设A(x1,y1),B(x2,y2),中点P(x0,y0).kOA=y1x1,kOB=y2x2. OA⊥OB,∴kOA·kOB=-1,∴x1x2+y1y2=0. y12=2px1,y22=2px2,∴y122p·y222p+y1y2=0 y1≠0,y2≠0,∴y1y2=-4p2,...