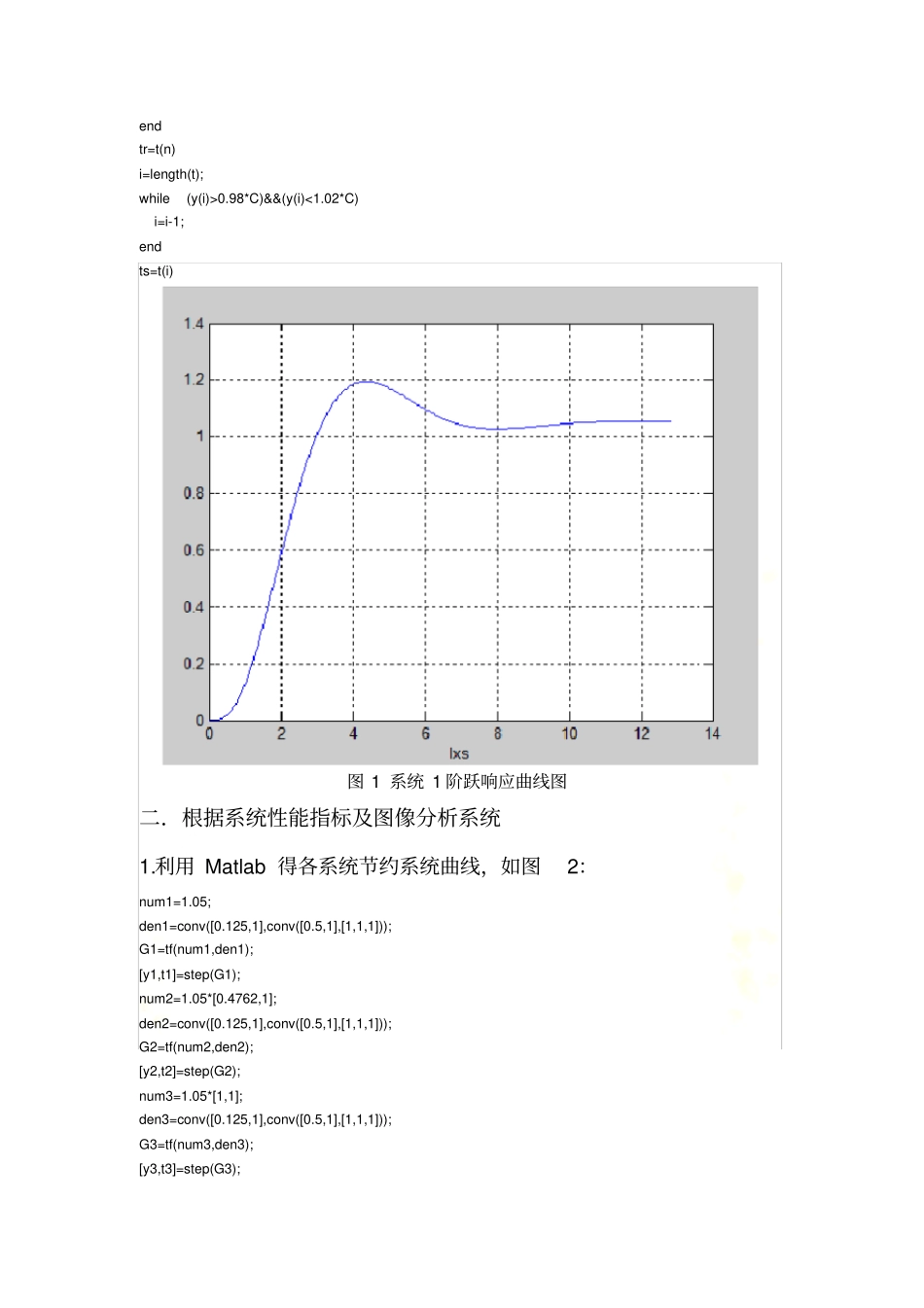
利用 matlab 分析系统动态性能控制系统的时域分析一.系统阶跃响应的性能指标表 1 系统性能指标序号系统tr tp Mp ts 11.05(0.125s+1)(0.5s+1)(s^2+s+1)3.1915 4.3520 13.7885 8.4968 2 1.05(0.4762s+1)(0.125s+1)(0.5s+1)(s^2+s+1)2.6229 3.7770 15.9147 8.1835 3 1.05(s+1)(0.125s+1)(0.5s+1)(s^2+s+1)1.9481 3.1500 25.3370 8.0824 4 1.05(0.4762s+1)(0.25s+1)(0.5s+1)(s^2+s+1)2.8328 3.9869 15.4635 8.2885 5 1.05(0.4762s+1)(0.5s+1)(s^2+s+1)2.5180 3.6721 16.0505 8.0786 6 1.05s^2+s+12.5180 3.6721 16.2874 7.9737 利用 matlab 程序求出各系统阶跃响应的性能指标及图像,如求原系统 1 的方程:num=1.05;den=conv([0.125,1],conv([0.5,1],[1,1,1]));G=tf(num,den);C=dcgain(G);[y,t]=step(G);plot(t,y)grid[Y,K]=max(y);tp=t(K)mp=100*(Y-C)/Cn=1;while y(n)0.98*C)&&(y(i)<1.02*C) i=i-1;endts=t(i) 图 1 系统 1 阶跃响应曲线图二.根据系统性能指标及图像分析系统1.利用 Matlab 得各系统节约系统曲线,如图2:num1=1.05;den1=conv([0.125,1],conv([0.5,1],[1,1,1]));G1=tf(num1,den1);[y1,t1]=step(G1);num2=1.05*[0.4762,1];den2=conv([0.125,1],conv([0.5,1],[1,1,1]));G2=tf(num2,den2);[y2,t2]=step(G2);num3=1.05*[1,1];den3=conv([0.125,1],conv([0.5,1],[1,1,1]));G3=tf(num3,den3);[y3,t3]=step(G3);num4=1.05*[0.4762,1];den4=conv([0.25,1],conv([0.5,1],[1,1,1]));G4=tf(num4,den4);[y4,t4]=step(G4);num5=1.05*[0.4762,1];den5=conv([0.5,1],[1,1,1]);G5=tf(num5,den5);[y5,t5]=step(G5);num6=1.05;den6=[1,1,1];G6=tf(num6,den6);[y6,t6]=step(G6);plot(t1,y1,t2,y2,t3,y3,t4,y4,t5,y5,t6,y6);grid;xlabel('lxs') 图 2 2. 如图 3 所示,系统加入零点后, 阶跃响应的上升时间和调节时间均减小,起到了响应加速的作用; 但造成原超调量增大, 影响了系统的平稳性。图 3 3. 如图 4 所示,图 4 系统 3 的零点在系统 2 的零点的右侧,响应的上升时间及调节时间更短,明显提高了系统速度; 但是超调量与系统2 相比更大, 严重影响了系统的平稳性。4. 如图 5 所示,图 5 系统 4 与系统 2 相比,响应时间变长, 影响了系统加速响应, 但超调量变小,平稳性变好;系统5 与系统 2 相比,响应时间变短,一定程度上改善了系统响应的快速性,但超调量变大,平稳性变差。5. 如图 6 所示,系统 5、6 与系统 1 相比,响应时间变短,超调量相差无几,因此相距很近的零极点可以改善系统响应的快速性,是系统加速。图 6