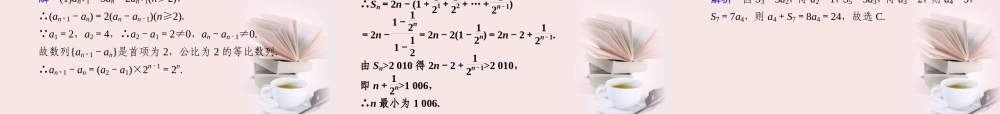§2 数列的综合应用 真题热身 1.(2011·四川)数列{an}的首项为 3,{bn}为等差数列且 bn= an+1-an(n∈N*).若 b3=-2,b10=12,则 a8 等于( ) A.0 B.3 C.8 D.11 解析 设数列{bn}的首项为 b1,公差为 d,由 b3=-2,b10=12, 得 b1+2d=-2,b1+9d=12,解得 b1=-6,d=2, ∴bn=-6+2(n-1)=2n-8. bn=an+1-an, ∴a8=(a8-a7)+(a7-a6)+(a6-a5)+(a5-a4)+(a4-a3)+ (a3-a2)+(a2-a1)+a1 =b7+b6+b5+…+b1+a1=7×(-6+2×7-8)2+3=3. B2.(2011·江西)已知数列{an}的前 n 项和 Sn 满足:Sn+Sm= Sn+m,且 a1=1,那么 a10 等于 ( ) A.1 B.9 C.10 D.55 解析 Sn+Sm=Sn+m,a1=1,∴S1=1. 可令 m=1,得 Sn+1=Sn+1, ∴Sn+1-Sn=1. 即当 n≥1 时,an+1=1, ∴a10=1. A3.(2011·广东)已知{an}是递增等比数列,a2=2,a4-a3=4, 则此数列的公比 q=________. 解析 由 a2=2,a4-a3=4 得方程组 a2=2,a2q2-a2q=4 ⇒ q2- q-2=0, 解得 q=2 或 q=-1. 又{an}是递增等比数列,故 q=2. 2 4.(2011·浙江)若数列{n(n+4)(23)n}中的最大项是第 k 项,则 k =________. 解析 由题意知 k(k+4)(23)k≥(k-1)(k+3)(23)k-1,k(k+4)(23)k≥(k+1)(k+5)(23)k+1, 解得 10≤k≤1+ 10. k∈N*,∴k=4. 4考点整合 1.根据数列的递推关系求数列的通项公式 (1)利用递推关系写出前几项,根据前几项的特点观察、归纳猜想出 an的表达式,然后用数学归纳法证明. (2)当已知数列{an}中,满足 an+1-an=f(n),且 f(1)+f(2)+… +f(n)可求,则可用累加法求数列的通项 an. (3)当已知数列{an}中,满足an+1an =f(n),且 f(1)·f(2)·…·f(n) 可求,则可用累积法求数列的通项 an. (4)将递推关系进行变换,转化为常见数列(等差数列、等比 数列). 2.常见的数列求和的方法 (1)公式法求和 适合求等差数列或等比数列的前 n 项和.对等比数列利用 公式法求和时,一定注意公式 q 是否能取 1. (2)错位相减法 这是推导等比数列的前 n 项和公式时所用的方法,主要用于求数列{anbn}的前 n 项和,其中{an}、{bn}分别是等差数列和等比数列. (3)裂项相消法 把数列和式中的各项分别裂开后,消去一部分从而计算和的方法,适用于求通项为...