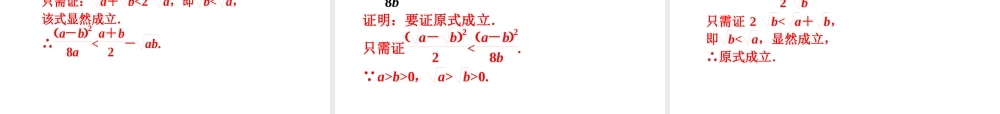§6.3 不等式的证明考点探究 · 挑战高考考向瞭望 · 把脉高考6.3不等式的证明双基研习 · 面对高考证明不等式的三种常用方法1 .比较法(1) 作差比较法① 理论依据: a>b⇔ _______ ; a0a - b<0(2)作商比较法 ①理论依据:b>0,ab>1⇒ ______; b<0,ab>1⇒ _______. ②证明步骤:作商→变形→判断与 1 的大小关系. a>bax B . x2 + 2>2xC . x2 + 3>3x D . x2 + 4>4x2.已知 a,b 为非零实数,且 a>b,则下列不等式一定成立的是( ) A.a2>b2 B.1a<1b C.|a|>|b| D.2a>2b 答案: D答案: D3 . 已 知 a < 0 , - 1 < b < 0 , 则( )A . a > ab > ab2 B . ab2 > ab > aC . ab > a > ab2 D . ab > ab2 > a4.若 ab>0,则ba+ab________2. 答案:≥5 .设 x = a2b2 + 5 , y = 2ab - a2 - 4a ,若 x>y , 则 实 数 a , b 应 满 足 的 条 件 为________ .答案: ab≠1 或 a≠ - 2考点探究 · 挑战高考考点突破比较法(1) 用作差比较法证明不等式时,通常是进行因式分解或利用各因式的符号比较法进行判断,或配方利用非负数的性质进行判断.(2) 作商法要弄清分母的符号,再将商式变形与 1比较.参...