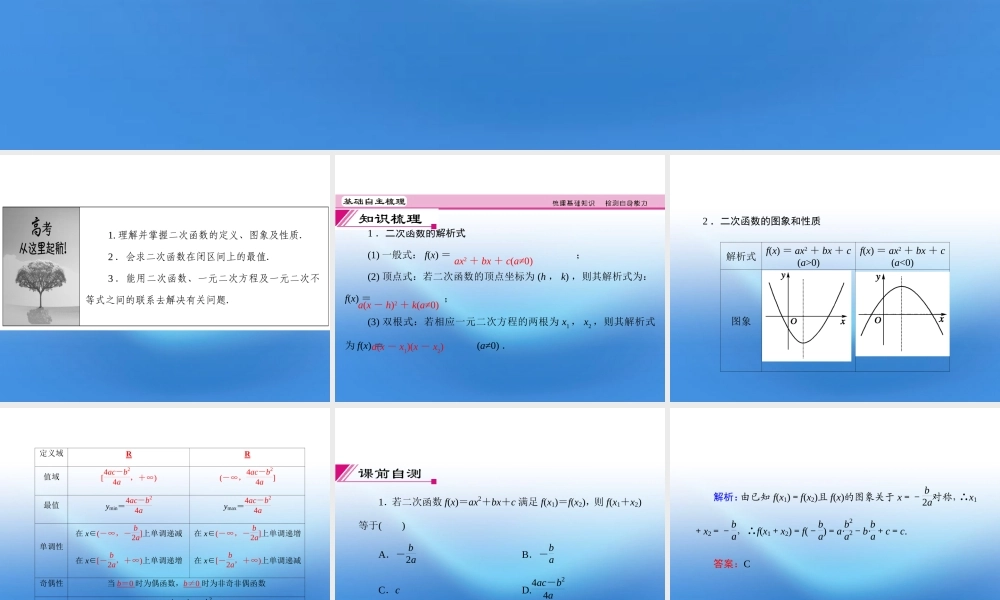
第四节 二次函数1. 理解并掌握二次函数的定义、图象及性质.2 .会求二次函数在闭区间上的最值.3 .能用二次函数、一元二次方程及一元二次不等式之间的联系去解决有关问题.1 .二次函数的解析式(1) 一般式: f(x) =;(2) 顶点式:若二次函数的顶点坐标为 (h , k) ,则其解析式为:f(x) =;(3) 双根式:若相应一元二次方程的两根为 x1 , x2 ,则其解析式为 f(x) =(a≠0) .ax2 + bx + c(a≠0)a(x - h)2 + k(a≠0)a(x - x1)(x - x2)2 .二次函数的图象和性质解析式f(x) = ax2 + bx + c(a>0)f(x) = ax2 + bx + c(a<0)图象定义域 R R 值域 [4ac-b24a,+∞) (-∞,4ac-b24a] 最值 ymin=4ac-b24a ymax=4ac-b24a 单调性 在 x∈(-∞,- b2a]上单调递减 在 x∈[- b2a,+∞)上单调递增 在 x∈(-∞,- b2a]上单调递增 在 x∈[- b2a,+∞)上单调递减 奇偶性 当 b=0 时为偶函数,b≠0 时为非奇非偶函数 顶点 (- b2a,4ac-b24a) 对称性 图象关于直线 x=- b2a成轴对称图形 1.若二次函数 f(x)=ax2+bx+c 满足 f(x1)=f(x2),则 f(x1+x2)等于( ) A.- b2a B.-ba C.c D.4ac-b24a 解析:由已知 f(x1)=f(x2)且 f(x)的图象关于 x=- b2a对称,∴x1+x2=-ba,∴f(x1+x2)=f(-ba)=a·b2a2-b·ba+c=c. 答案:C 2 .若函数 f(x) = (a - 1)x2+ (a2- 1)x + 1 是偶函数,则在区间[0∞,+) 上 f(x) 是 ( )A .减函数B .增函数C .常函数D .可能是减函数,也可能是常函数解析: f(x) 为偶函数,∴ a2- 1 = 0 ,即 a = ±1 ,当 a = 1 时, f(x) = 1 为常函数.当 a =- 1 时, f(x) =- 2x2+ 1 ,在 [0 ,+∞ ) 上为减函数.答案: D3 .函数 f(x) = 4x2 - mx + 5 在区间 [ - 2∞,+) 上是增函数,则 f(1) 的取值范围是 ( )A . f(1)≥25 B . f(1) = 25C . f(1)≤25 D . f(1)>25解析:由题意知m8≤-2,∴m≤-16, ∴f(1)=9-m≥25. 答案:A 4 .已知函数 f(x) = x2 - 2x + 2 的定义域和值域均为 [1 , b] ,则 b = ( )A . 3 B . 2 或 3C . 2 D . 1 或 2解析: f(x) = (x - 1)2+ 1 ,∴f(x) 在 [1 , b] 上是增函数, f(x)max...