河北省高考数学第一轮总复习知识点检测 5.6三角函数的图象与性质(Ⅱ)课件 旧人教版 课件VIP免费

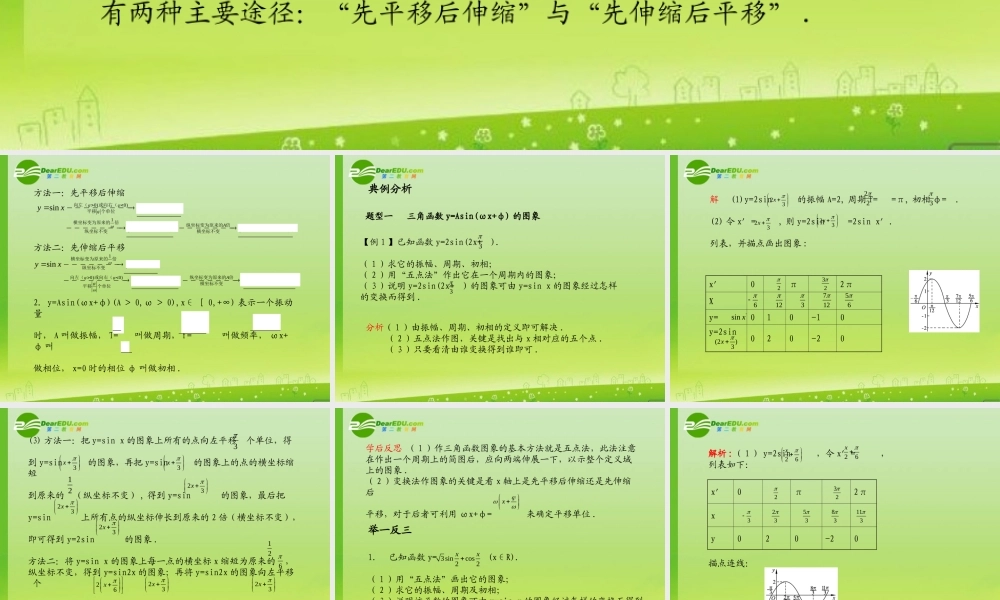
第六节 三角函数的图象与性质（Ⅱ）基础梳理1. 作 y=Asin(ωx+φ) 的图象主要有以下两种方法：（ 1 ）用“五点法”作图 .用“五点法”作 y=Asin(ωx+φ) 的简图，主要是通过变量代换，设z=ωx+φ, 由 z 取 0 ， ,π, ,2π 来求出相应的 x ，通过列表，计算得出五点坐标，描点后得出图象 .（ 2 ）由函数 y=sin x 的图象通过变换得到 y=Asin(ωx+φ) 的图象 ,有两种主要途径：“先平移后伸缩”与“先伸缩后平移” .232方法一：先平移后伸缩方法二：先伸缩后平移2. y=Asin(ωx+φ)(A ＞ 0,ω ＞ 0),x∈ ［ 0,+∞) 表示一个振动量时， A 叫做振幅， T= 叫做周期， f= 叫做频率， ωx+φ 叫做相位， x=0 时的相位 φ 叫做初相 .0)0)sinsin()yxyx       向左（或向右（平移个单位1sin()sin().AyxyAx            横坐标变为原来的倍纵坐标变为原来的 倍纵坐标不变横坐标不变1sinsinyxyx      横坐标变为原来的倍纵坐标不变0)0)sin()sin().AyxyAx             向左（或向右（纵坐标变为原来的 倍横坐标不变平移个单位212T典例分析题型一 三角函数 y=Asin(ωx+φ) 的图象分析（ 1 ）由振幅、周期、初相的定义即可解决 . （ 2 ）五点法作图，关键是找出与 x 相对应的五个点 . （ 3 ）只要看清由谁变换得到谁即可 .【例 1 】已知函数 y=2sin(2x+ ).（ 1 ）求它的振幅、周期、初相；（ 2 ）用“五点法”作出它在一个周期内的图象；（ 3 ）说明 y=2sin(2x+ ) 的图象可由 y=sin x 的图象经过怎样的变换而得到 .33解 (1)y=2sin 的振幅 A=2, 周期 T= =π, 初相 φ= .(2) 令 x′= , 则 y=2sin =2sin x′.列表，并描点画出图象 :23x22323x23xx′0π2πXy=010-10y=2sin 020-20323261271256'sin x(2)3x(3) 方法一：把 y=sin x 的图象上所有的点向左平移 个单位，得到 y=sin 的图象，再把 y=sin 的图象上的点的横坐标缩短到原来的 （纵坐标不变） , 得到 y=sin 的图象，最后把y=sin 上所有点的纵坐标伸长到原来的 2 倍（横坐标不变...