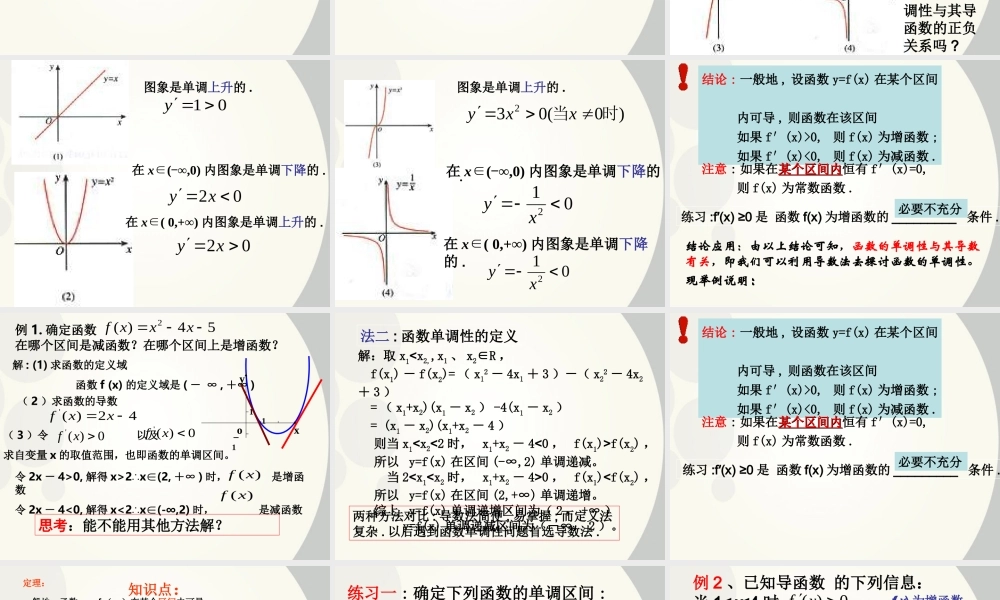
复习 1 、 某点处导数的定义——这一点处的导数即为这一点处切线的斜率Δx)f(xΔx)f(xlim)(xf000Δx02 、 某点处导数的几何意义—— 引例、 已知函数 y=2x3-6x2+7,求证:这个函数在区间 (0,2) 上是单调递减的 . 问题:怎样利用函数单调性的定义来讨论或证明其在定义域的单调性 判断函数单调性的常用方法:( 1 )定义法 (2) 图象法 一般地,设函数 y = f(x) 的定义域为 A ,区间 I A . 如果对于区间 I 内的任意两个值 x1 、 x2 ,当 x1 < x2 时,都有 f(x1) < f(x2) ,那么就说 y = f(x) 在区间 I 上是单调增函数, I 称为 y = f(x) 的单调增区间. 如果对于区间 I 内的任意两个值 x1 、 x2 ,当 x1 < x2时,都有 f(x1) > f(x2) ,那么就说 y = f(x) 在区间 I 上是单调减函数, I 称为 y = f(x) 的单调减区间. 若函数 y = f(x) 在区间 I 上是单调增函数或单调减函数,那么就说函数 y = f(x) 在区间 I 上具有单调性.单调增区间和单调减区间统称为单调区间. 1 、单调增函数与单调减函数区间 I任意当 x1 < x2 时,都有 f(x1) < f(x2)2 、单调性、单调区间一、复习回顾: 2 .由定义证明函数的单调性的一般步骤: (1) 设 x1 、 x2 是给定区间的任意两个值, 且 x1< x2. (2) 作差 f(x1) - f(x2) ,并变形 . (3) 判断差的符号,从而得函数的单调性 .发现问题:用单调性定义讨论函数单调性虽然可行,但十分麻烦,尤其是在不知道函数图象时 . 探究 : 观察下列图象的单调区间 ,并求单调区间相应的导数 . 探究 :①观察下列 4个函数的图象 , 写出它们的单调区间 , 并求出每个区间导数的正负 . ② 你能得出函数的单调性与其导函数的正负关系吗 ? 02 xy02 xy在 x(∈ -∞,0) 内图象是单调下降的 .在 x( 0,+∞)∈内图象是单调上升的 .图象是单调上升的 .01y 图象是单调上升的 .)0(032时当 xxy012 xy012 xy.在 x(∈ -∞,0) 内图象是单调下降的在 x( 0,+∞)∈内图象是单调下降的 . 结论 : 一般地 , 设函数 y=f(x) 在某个区间 内可导 , 则函数在该区间 如果 f′(x)>0, 则 f(x) 为增函数 ; 如果 f′(x)<0, 则 f(x) 为减函数 .结论应用:由以上结论可知,函数的单调性与其导数有关,即我们可...