河北省高考数学第一轮总复习知识点检测 3.2指数与指数函数课件 旧人教版 课件VIP免费

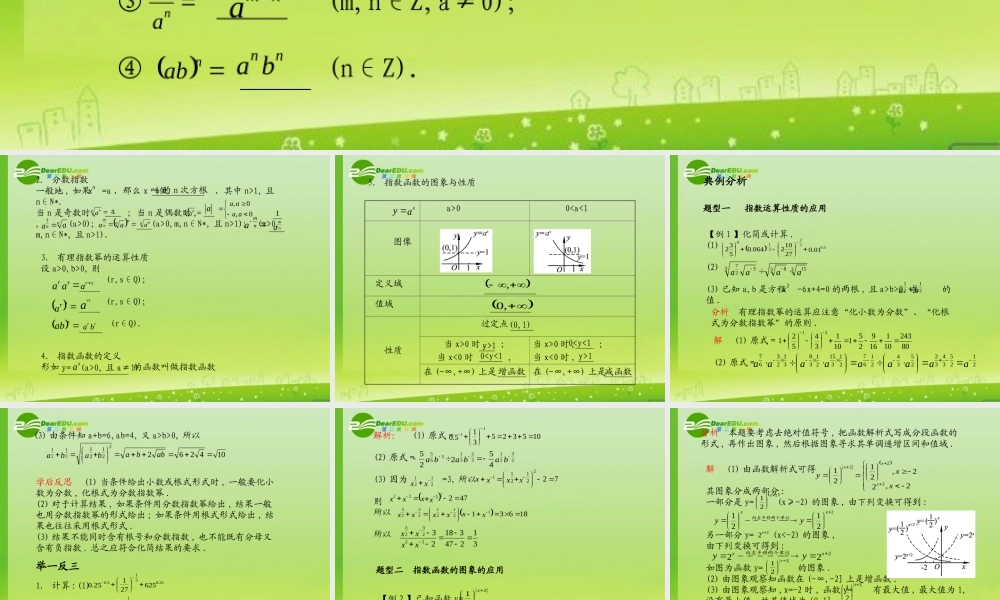
第二节 指数与指数函数基础梳理1. 整数指数(1) 整数指数幂概念 :① =a·a·…·a(n 个 a ） (n∈N*);② = (a≠0); ③ (a≠0,n∈N*).(2) 整数指数幂的运算性质 :① (m,n∈Z);② (m,n∈Z);③ (m,n∈Z,a≠0);④ (n∈Z).ana0aanmanm  am namnaanmanm abnbannanan112. 分数指数一般地 , 如果 =a ，那么 x 叫做 ，其中 n>1, 且n∈N*.当 n 是奇数时 , ；当 n 是偶数时 ,, (a>0); (a>0,m,n∈N*, 且 n>1); (a>0,m,n∈N*, 且 n>1).xnnnaa 13. 有理指数幂的运算性质设 a>0,b>0, 则 (r,s∈Q); (r,s∈Q); (r∈Q).4. 指数函数的定义形如 的函数叫做指数函数 axa 的 n 次方根nnaanna0,0,aaaaa  n aamnmnmaanma nm1aasrasr  ar ssra abrbarry= (a>0, 且 a≠1)5. 指数函数的图象与性质 a>0 00 时 , ;当 x<0 时 ,当 x>0 时 , ;当 x<0 时 , 在 (-∞,+∞) 上是 在 (-∞,+∞) 上是ayx,,0y>101增函数减函数(0,1)典例分析题型一 指数运算性质的应用【例 1 】化简或计算 .(1)(2)(3) 已知 a,b 是方程 -6x+4=0 的两根 , 且 a>b>0, 求 的值 .01.027102064.05325.032310315383327aaaax2ba2121 分析 有理指数幂的运算应注意“化小数为分数”、“化根式为分数指数幂”的原则 .解 (1) 原式 =(2) 原式 =802431011692511013452121aaaaaaaaa2125343225342167213152138312367(3) 由条件知 a+b=6,ab=4, 又 a>b>0, 所以104262212122121abbababa学后反思 (1) 当条件给出小数或根式形式时 , 一般要化小数为分数 , 化根式为分数指数幂 .(2) 对于计算结果 , 如果条件用分数指数幂给出 , 结果一般也用分数指数幂的形式给出 ; 如果条件用根式形式给出 , 结果也往往采用根式形式 .(3) 结果不能同时含有根号和分数指数 , 也不能既有分母又含有负指数 . 总之应符合化简结果的要求 .举一反三1. 计算 :(1)(2)(3) 若 =3, 求 的值 . 62527125.025.0315.0...