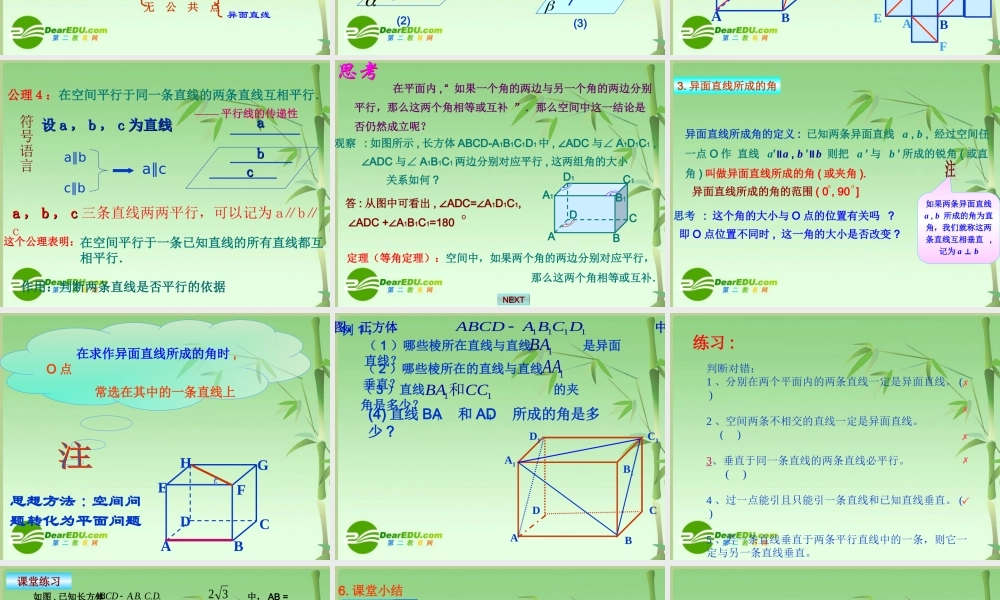
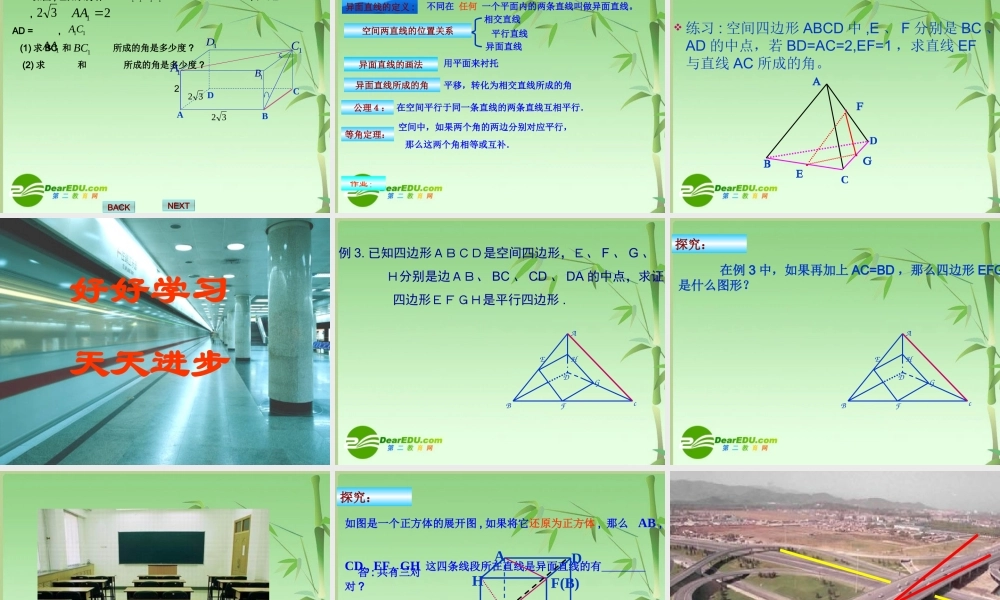
同一平面内的两条直线有几种位置关系?相交直线平行直线相交直线(有一个公共点)平行直线(无公共点)aboab BACK1. 异面直线的定义 :不同在 任何 一个平面内的两条直线叫做异面直线。 判断异面直线的方法:1) 定义2) 既不平行也不相交 按是否共面分同在一个平面内相交直线平行直线 不同在任何一个平面内 :异面直线 有一个公共点 : 按公共点个数分相交直线无 公 共 点平行直线异面直线 2.1.2 空间中直线与直线之间的位置关系 2. 异面直线的画法说明 : 画异面直线时 , 为了体现 它们不共面的特点。常借 助一个或两个平面来衬托 .如图:aabaAbb(1)(3)(2) 探究:如图是一个正方体的展开图 , 如果将它还原为正方体 , 那么 AF, BM , ED , DN 这四条线段所在直线是异面直线的有 对 ?D答 : 共有三对FECADBMNAN(M)FEDBC 公理4:在空间平行于同一条直线的两条直线互相平行.在空间平行于一条已知直线的所有直线都互相平行.这个公理表明:作用:判断两条直线是否平行的依据——— 平行线的传递性设设 aa ,, bb ,, cc 为直线为直线a∥bc∥ba∥caa ,, bb ,, cc 三条直线两两平行,可以记为 a∥b∥c符号语言aabbcc 在平面内 , “ 如果一个角的两边与另一个角的两边分别 平行,那么这两个角相等或互补 ”.那么空间中这一结论是 否仍然成立呢?定理(等角定理):空间中,如果两个角的两边分别对应平行, 那么这两个角相等或互补.观察 : 如图所示 , 长方体 ABCD-A1B1C1D1中 , ADC∠与∠ A1D1C1 , ∠ADC 与∠ A1B1C1两边分别对应平行 , 这两组角的大小 关系如何 ?答 : 从图中可看出 , ADC= A∠∠1D1C1, ∠ADC + A∠1B1C1=180OD1C1B1A1CABDNEXT 3. 异面直线所成的角异面直线所成角的定义 : 已知两条异面直线 a , b , 经过空间任一点 O 作 直线 a′∥a , b ′∥b 则把 a ′ 与 b ′ 所成的锐角 ( 或直角 ) 叫做异面直线所成的角 ( 或夹角 ).思考 : 这个角的大小与 O 点的位置有关吗 ? 即 O 点位置不同时 , 这一角的大小是否改变 ?异面直线所成的角的范围 ( 0 , 90 ]oo如果两条异面直线 a , b 所成的角为直角,我们就称这两条直线互相垂直 , 记为 a ⊥ b 在求作异面直线所成的角时 ,O 点 常选在其中的一条直线上 ABGFHEDC思想方法 : 空间问题转化为平面问题 例 1 :ABCDA1B1C1D1 ...