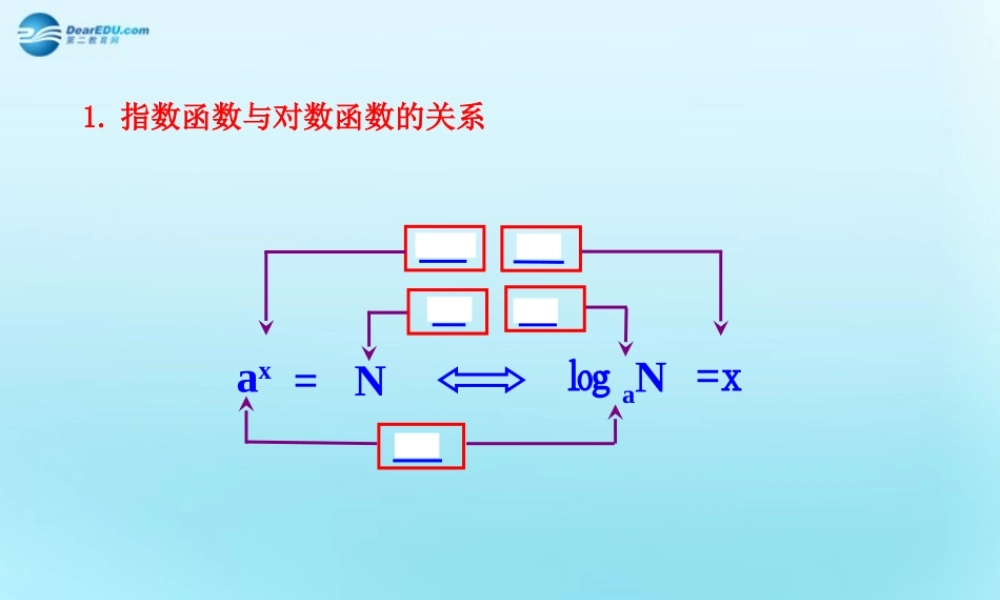
axN=㏒ aN =x幂指数幂值幂值真数底数1. 指数函数与对数函数的关系对数形式特 点记 法常用对数自然对数底数为 10底数为 elg Nln N2. 两种常用的对数3. 对数的运算法则若 a > 0 , a≠1 , M > 0,N > 0运算数学表达式自然语言积的对数商的对数幂的对数loga(MN)=logaM+logaNloga(N1•N2•…•Nk)=logaN1+logaN2+…+logaNk ( Ni >0 , i=1 , 2 ,…, k )正因数积的对数等于同一底数的各因数对数的和aaaMloglog Mlog NN 两个正数商的对数等于同一底数的被除数的对数减去除数的对数logaMα=αlogaM(α∈R)正数幂的对数等于幂指数乘以同一底数幂的底数的对数4. 对数函数的图象与性质底数图象定义域值域性质a>10
1 时, y>0.(3) 当 x>1 时, y<0.当 00.(2) 在 (0,+∞) 上是增函数(2) 在 (0,+∞) 上是减函数5. 指数函数与对数函数的联系与区别指数函数 y=ax(a > 0,a≠1)对数函数 y=logax(a > 0,a≠1)定义域值域图象x∈R x∈(0,+∞)y∈ ( 0 , +∞ )y∈R指数函数 y=ax(a > 0,a≠1)对数函数 y=logax(a > 0,a≠1)性质过定点( 0 , 1 )过定点( 1 , 0 )减函数增函数减函数增函数x∈(-∞ , 0)时, y∈(1,+∞)x∈(0,+∞) 时, y∈(0,1)x∈(-∞,0)时 ,y∈(0,1) x∈(0,+∞)时 ,y∈(1,+∞)x∈(0,1) 时,y∈(0,+∞) x∈(1,+∞)时 ,y∈(-∞,0)x∈(0,1) 时,y=∈(-∞,0) x∈(1,+∞) 时,y∈(0,+∞)0 < a < b < 1 0 < < 1>1> 1