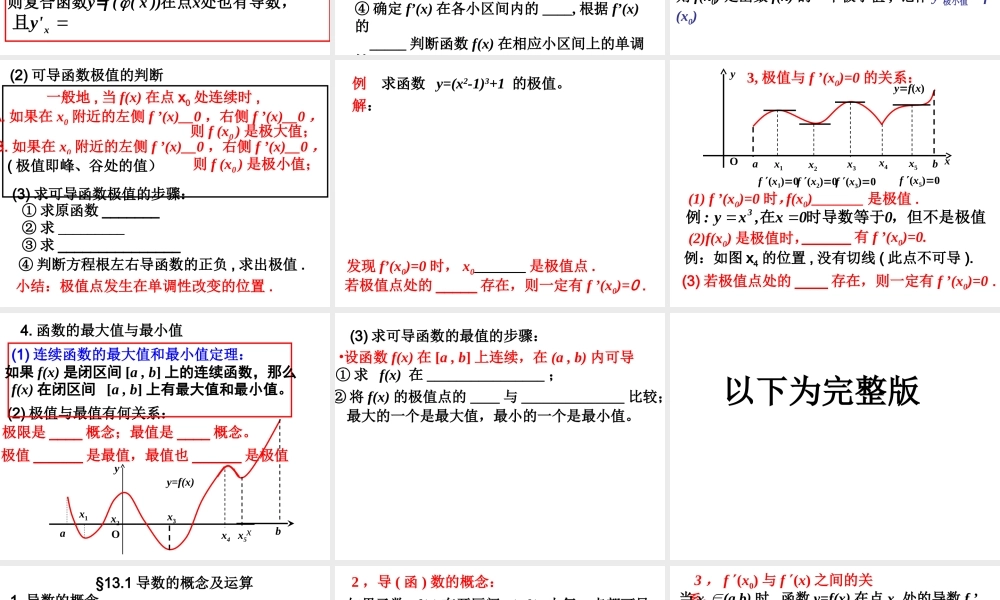
§13.1 导数的概念及运算(A) 函数 f(x) 在点 x0 处的导数的概念0f ( x )xyx如果函数在处的增量与自变量的增量的比值,00x0x0f ( xx )f ( x )yx0limlimxx 当时的极限存在,则称 y=f(x) 在点 x0 处可导,并称称此极限值为函数 y=f(x) 在 x0 处的导数 .00x xf ( x )y记'或作:(B) 由定义求点求函数 y=f(x) 在 x0 处的导数的方法:00f ( xx )f ( x )y( 2 ) ;xx算比值 x0y( 3 )ylim.x求极限 1. 导数的概念00xx0f ( x )f ( x )limxx 2 ,导 ( 函 ) 数的概念:这时,对于开区间 (a,b) 内每一个确定的值 x0 ,都对应着一个确定的导数 f ’(x0) ,这样就在开区间 (a,b) 内构成了一个新的函数,我们把这一新函数叫做 f(x) 在开区间 (a,b) 内的导函数,简称为导数,记作 :f ’(x)如果函数 f(x) 在开区间 (a,b) 内每一点都可导,就说 f(x) 在开区间 (a,b) 内可导.x(y' )需指明自变量时记作y' 或 3 , f (x0) 与 f (x) 之间的关系:当 x0(a,b)∈时 , 函数 y=f(x) 在点 x0 处的导数 f ’(x0) ,重要结论:如果函数 y=f(x) 在点 x0 处可导 , 那么函数 y=f(x) 在点 X0 处 ____.0)()(0xxxfxf等于 __________ 在点 x0 处的函数值。(2) 物体在 t0 时刻的瞬时速度 : (1) 曲线在 P(x0,y0) 的切线斜率 :4. 导数的实际意义:(3) 物体在 t0 时刻的瞬时加速度 : 5. 几种常见函数的导函数:公式 3 (sinx)’= 公式 4 (cosx)’= 公式 1 C’ = (C 为常数 )公式 2 (xn)’ = (nQ)∈(ln x )' a5 (log x )' 公式x6 ( a ) 公式x( e ) 6, 函数四则运算的导数:( uv ) (1) 和 ( 或差 ) 的导数 :(2) 积的导数 :( u v ) (3) 商的导数 :u() ;( v0 )v 7, 复合函数求导 :x,u( x )xu''( x ),一般地 设函数在 处有导数uyf ( u )xuy'f '( u ),函数在在点 的对应点 处有导数y f ( ( x ))x则复合函数 =在点 处也有导数,xy' 且 §13.2 导数的应用1. 函数的单调性(1) 一般地 , 设函数 y=f(x) 在某个区间内可导 ,f '( x )0如果 f '( x )0如果 (2) 利用结论求可导函数单调区间的一般步骤:① 求函...