高一数学三角函数图象的应用复习课 人教版0 课件VIP免费

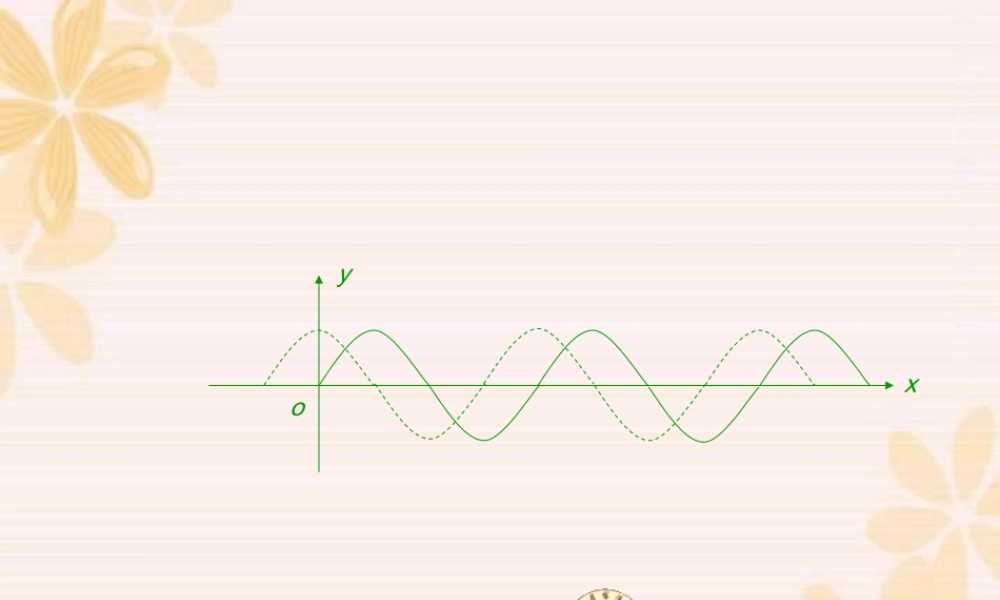
浙江省富阳中学xyo正弦曲线y = cos x, xR∈y = sin x, xR∈余弦曲线Ⅰ 、回顾正弦、余弦曲线回顾xyo1-2-234-13sin(2),3Ryxx画出函数的简图.xⅡ 、复习五点法作图323sin()x23x0232261237125603－3006123712563-3xy复习cos例1. 方程2解的个数是_____________xxⅢ 、应用举例-1xyo1-2-234lgsin方程解的个数是_____________xx无数个y = cos x, xR∈y = 2x, xR∈y = sin x, xR∈(10,1)(1, 0)3个y = lg x, x>0( )sin2 sin,0,2__________.例2. 函数的图象 与直线有且仅有两个不同的交点， 则 的取值范围是f xxx xykk3sin ,0,( )sin ,2分析：，x xf xx x3xyo21-113ko23sin 22sin1[0,]2若方程，在上有唯一解, 确定 的取值范围.xxaa 2sin(2)[0,]62分析___化简得：，xax26x62321161220212y41271210120x11222 或aa  yx2-2122356( ),( ),2sin0,,2sin30,____,34sin(3) 1,_______.33设函数的图象与直线及 轴所围成图形的面积称为函数在上的面积，已知函数在上的面积为则(1)在上的面积为(2)在上的面积为f xxa xbxf xa bynxnnyxyx已知：n2n x yoy = sin nx, xR∈2阴Sn323 x yoy = sin 3x, xR∈阴？S 1－ 11－ 1已知：323 x yoy = sin 3x, xR∈阴23S y = -sin 3x+1, xR∈323 x yo43123阴＋Ssincostan(0),21. 若则（ ） A. (0,) B. (,) C. (,) D. (,)66 44 33 2   2.( )2sin,3 4已知 是正数，函数在 上递增，求 的取值范围.f xx C30, 2余弦正弦 数学源于生活数学用于生活小结数形结合化归思想xyo234