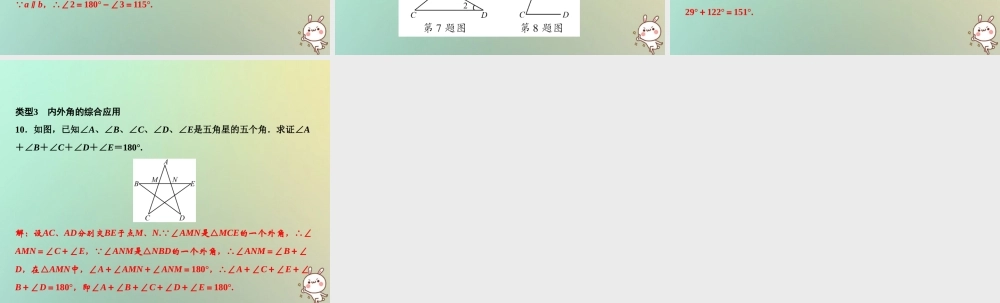
第七章 平行线的证明专题突破七 三角形内角、外角的计算与证明2018 秋季数学 八年级 上册 • B 类型1 三角形的内角和 1.(巴中中考)若一个三角形三个内角的度数之比为1∶2∶3,则这个三角形是( ) A.锐角三角形 B.等边三角形 C.钝角三角形 D.直角三角形 2.(宜宾中考)如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠1=70°,则∠BAC的大小为( ) A.30° B.40° C.50° D.70° D B 3.(成都中考)在△ABC中,∠A∶∠B∶∠C=2∶3∶4,则∠A的度数为 . 4.(青海中考)如图,在△ABC中,∠ABC与∠ACB的平分线相交于点D,若∠A=50°,则∠BDC= . 40° 115° 5.如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,求∠EFG的度数. 解:∵AB∥CD,∠FGE=40°,∴∠AEG=140°,又∵EF平分∠AEG,∴∠FEG=70°,∵∠FGE=40°,∠FEG=70°,∴∠EFG=180°-70°-40°=70°. 6.(山西中考)如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,求∠2的度数. 解:∵∠1=55°,∴∠AED=55°,∵∠A=60°,∴∠ADE=65°=∠3,又∵a∥b,∴∠2=180°-∠3=115°. 类型2 三角形的外角 7.如图所示,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是 . 8.(邵阳中考)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为 . 70° 40° 9.(泰州中考)如图,AB∥CD,∠1=58°,FG平分∠EFD,求∠FGB的度数. 解:∵AB∥CD,∠1=58°,∴∠EFD=∠1=58°,∠GEF=122°,又∵FG平分∠EFD,∴∠EFG=29°,∵∠FGB是△EFG的外角,∴∠FGB=29°+122°=151°. 类型3 内外角的综合应用 10.如图,已知∠A、∠B、∠C、∠D、∠E是五角星的五个角.求证∠A+∠B+∠C+∠D+∠E=180°. 解:设AC、AD分别交BE于点M、N.∵∠AMN是△MCE的一个外角,∴∠AMN=∠C+∠E,∵∠ANM是△NBD的一个外角,∴∠ANM=∠B+∠D,在△AMN中,∠A+∠AMN+∠ANM=180°,∴∠A+∠C+∠E+∠B+∠D=180°,即∠A+∠B+∠C+∠D+∠E=180°.