高中数学 第2章242抛物线的简单几何性质课件 新人教A版选修2-1 课件VIP免费

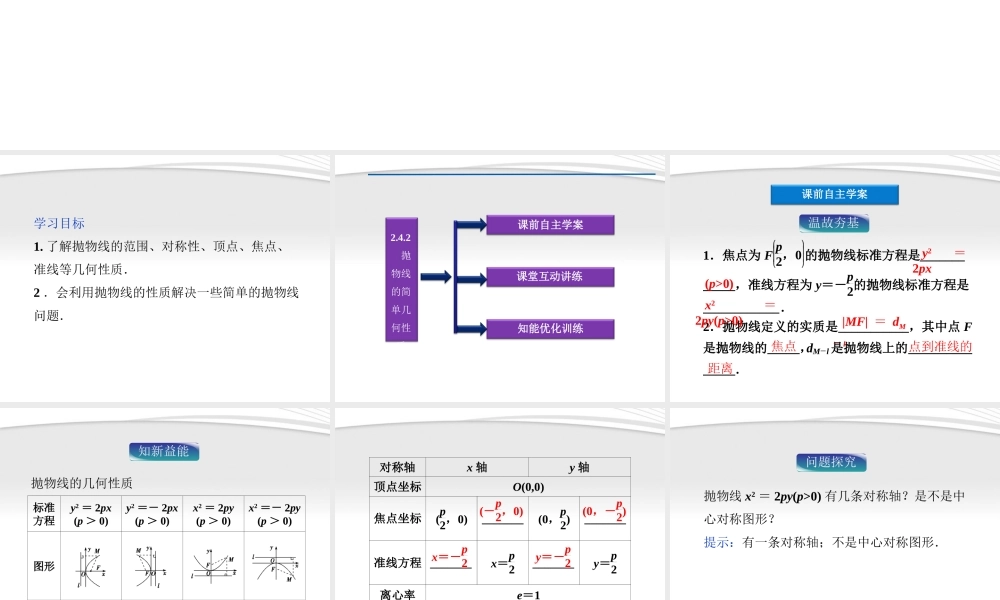
2 ． 4.2 抛物线的简单几何性质学习目标1. 了解抛物线的范围、对称性、顶点、焦点、准线等几何性质．2 ．会利用抛物线的性质解决一些简单的抛物线问题．课堂互动讲练知能优化训练2.4.2 抛物线的简单几何性质课前自主学案课前自主学案温故夯基1．焦点为 Fp2，0 的抛物线标准方程是_______ _____，准线方程为 y＝－p2的抛物线标准方程是____________． 2．抛物线定义的实质是___________，其中点 F是抛物线的_____，dM－l 是抛物线上的__________ _____． y2＝2px(p>0)x2＝2py(p>0)|MF| ＝ dM－ l焦点点到准线的距离知新益能抛物线的几何性质标准方程y2 ＝ 2px(p ＞ 0)y2 ＝－ 2px(p ＞ 0)x2 ＝ 2py(p ＞ 0)x2 ＝－ 2py(p ＞ 0)图形范围x≥0x≤0y≥0y≤0对称轴 x 轴 y 轴 顶点坐标 O(0,0) 焦点坐标 (p2，0) _______ (0，p2) _______ 准线方程 _______ x＝p2 _______ y＝p2 离心率 e＝1 (－p2，0) (0，－p2) x＝－p2 y＝－p2 问题探究抛物线 x2 ＝ 2py(p>0) 有几条对称轴？是不是中心对称图形？提示：有一条对称轴；不是中心对称图形．课堂互动讲练抛物线性质的应用考点突破抛物线的几何性质在解与抛物线有关的问题时具有广泛的应用，但是在解题的过程中又容易忽视这些隐含的条件． 已知抛物线的焦点 F 在 x 轴上，直线 l 过F 且垂直于 x 轴， l 与抛物线交于 A 、 B 两点， O 为坐标原点，若△ OAB 的面积等于 4 ，求此抛物线的标准方程．例例 11【思路点拨】 设抛物线方程y2＝2pxp≠0→ 求A、B两点的坐标→ 求出弦长AB→ 写出△OAB的面积，利用面积列方程解p→ 得结果 【解】 由题意，抛物线方程为 y2＝2px(p≠0)， 焦点 Fp2，0 ，直线 l：x＝p2， ∴A、B 两点坐标为p2，p ，p2，－p ，∴|AB|＝2|p|. △OAB 的面积为 4， ∴12·|p2|·2|p|＝4，∴p＝±2 2. ∴抛物线方程为 y2＝±4 2x. 变式训练 已知抛物线的顶点在坐标原点，对称轴为 x 轴，且与圆 x2＋y2＝4 相交于 A、B 两点，|AB|＝2 3，求抛物线方程． 解：由已知抛物线的焦点可能在 x 轴正半轴上，也可能在负半轴上．故可设抛物线方程为 y2 ＝ ax(a≠0) ．设抛物线与圆 x2 ＋ y2 ＝ 4 的交点为 A(x1 ， y1) ，B(x2 ， y2) ． 抛物线 y2 ＝ ax(a≠0) 与圆 x2 ＋...