高一数学 平面与平面平行的判定定理课件VIP免费

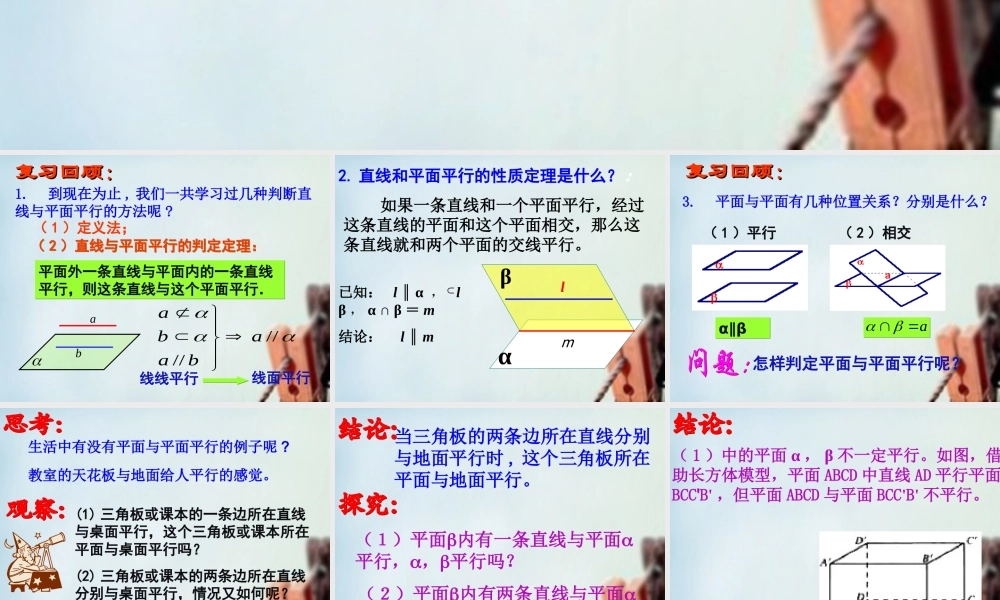
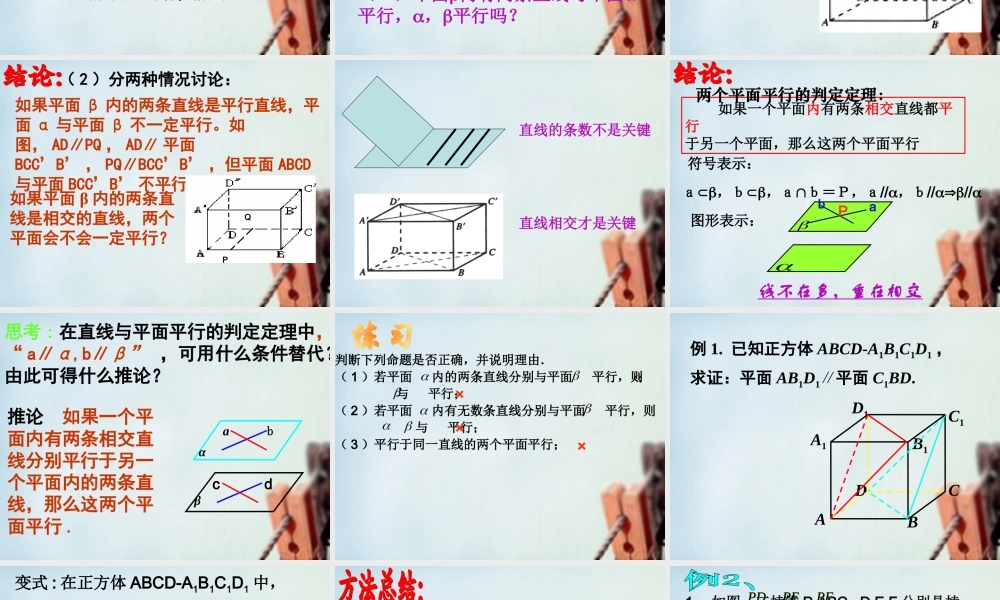
高一数学必修二 2.2.2 平面与平面平行的判定 2.2.2 平面与平面平行的判定 abPabP复习回顾：复习回顾：平面外一条直线与平面内的一条直线平行，则这条直线与这个平面平行．平面外一条直线与平面内的一条直线平行，则这条直线与这个平面平行．（ 2 ）直线与平面平行的判定定理：（ 2 ）直线与平面平行的判定定理：（ 1 ）定义法；ba////abaab线线平行线面平行1. 到现在为止 , 我们一共学习过几种判断直线与平面平行的方法呢 ?2. 直线和平面平行的性质定理是什么？：已知： l ∥ α ， l β ， α ∩ β ＝ m 结论： l ∥ m ∩ αβ lm 如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和两个平面的交线平行。（ 1 ）平行（ 2 ）相交α∥βα∥βaa复习回顾：复习回顾：怎样判定平面与平面平行呢？3. 平面与平面有几种位置关系？分别是什么？生活中有没有平面与平面平行的例子呢 ?(1) 三角板或课本的一条边所在直线与桌面平行，这个三角板或课本所在平面与桌面平行吗？(2) 三角板或课本的两条边所在直线分别与桌面平行，情况又如何呢？教室的天花板与地面给人平行的感觉。当三角板的两条边所在直线分别与地面平行时 , 这个三角板所在平面与地面平行。（１）平面内有一条直线与平面平行，，平行吗？（２）平面内有两条直线与平面平行，，平行吗？（ 1 ）中的平面 α ， β 不一定平行。如图，借助长方体模型，平面 ABCD 中直线 AD 平行平面BCC'B' ，但平面 ABCD 与平面 BCC'B' 不平行。（ 2 ）分两种情况讨论：如果平面 β 内的两条直线是平行直线，平面 α 与平面 β 不一定平行。如图， AD∥PQ ， AD∥ 平面BCC’B’ ， PQ∥BCC’B’ ，但平面 ABCD与平面 BCC’B’ 不平行。PQ如果平面 β 内的两条直线是相交的直线，两个平面会不会一定平行？直线的条数不是关键直线相交才是关键 如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行 两个平面平行的判定定理：线不在多，重在相交符号表示： ａ，ｂ，ａｂ＝Ｐ，ａ，ｂ图形表示：abP思考 : 在直线与平面平行的判定定理中，“ a∥α,b∥β” ，可用什么条件替代？由此可得什么推论？推论 如果一个平面内有两条相交直线分别平行于另一个平面内的两条...