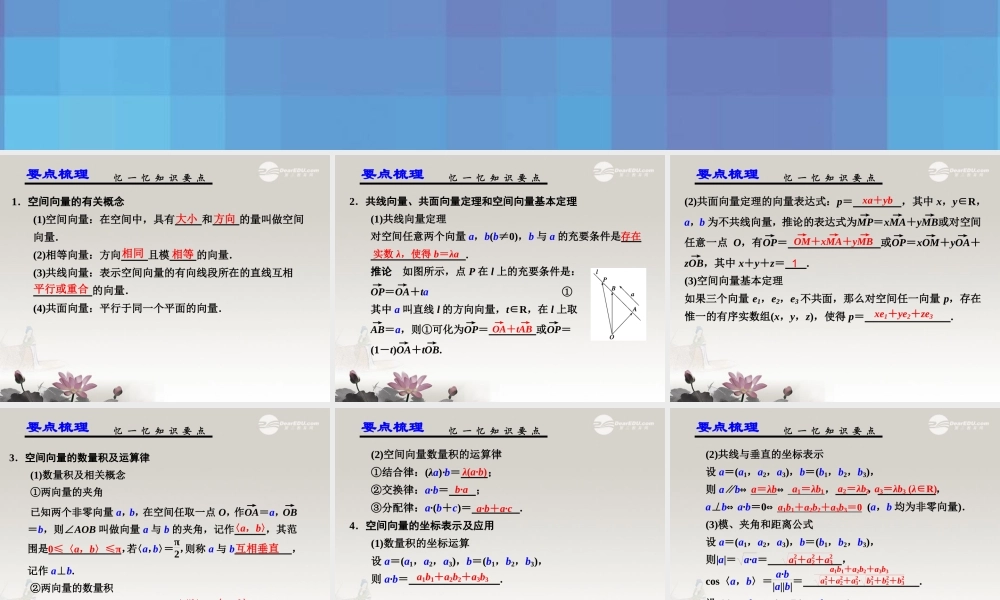
一轮复习讲义一轮复习讲义空间向量及其运算 1.空间向量的有关概念 (1)空间向量:在空间中,具有 和 的量叫做空间 向量. (2)相等向量:方向 且模 的向量. (3)共线向量:表示空间向量的有向线段所在的直线互相 的向量. (4)共面向量:平行于同一个平面的向量. 忆 一 忆 知 识 要 点大小 方向 相同 相等 平行或重合 要点梳理2.共线向量、共面向量定理和空间向量基本定理 (1)共线向量定理 对空间任意两个向量 a,b(b≠0),b 与 a 的充要条件是 . 推论 如图所示,点 P 在 l 上的充要条件是: OP→ =OA→ +ta ① 其中 a 叫直线 l 的方向向量,t∈R,在 l 上取 AB→ =a,则①可化为OP→ = 或OP→ = (1-t)OA→ +tOB→ . 忆 一 忆 知 识 要 点存在 实数 λ,使得 b=λa OA→ +tAB→ 要点梳理(2)共面向量定理的向量表达式:p= ,其中 x,y∈R,a,b 为不共线向量,推论的表达式为MP→ =xMA→ +yMB→ 或对空间任意一点 O,有OP→ = 或OP→ =xOM→ +yOA→ +zOB→ ,其中 x+y+z= . (3)空间向量基本定理 如果三个向量 e1,e2,e3 不共面,那么对空间任一向量 p,存在惟一的有序实数组(x,y,z),使得 p= . 忆 一 忆 知 识 要 点OM→ +xMA→ +yMB→ 1xe1+ye2+ze3 xa+yb 要点梳理3.空间向量的数量积及运算律 (1)数量积及相关概念 ①两向量的夹角 已知两个非零向量 a,b,在空间任取一点 O,作OA→ =a,OB→=b,则∠AOB 叫做向量 a 与 b 的夹角,记作 ,其范围是 ,若〈a,b〉=π2,则称 a 与 b ,记作 a⊥b. ②两向量的数量积 已知空间两个非零向量 a,b,则 叫做向量 a,b 的数量积,记作 ,即 . 忆 一 忆 知 识 要 点〈a,b〉 0≤〈a,b〉≤π 互相垂直 |a||b|cos〈a,b〉 a·b a·b=|a||b|cos〈a,b〉 要点梳理(2)空间向量数量积的运算律 ①结合律:(λa)·b= ; ②交换律:a·b= ; ③分配律:a·(b+c)= . 4.空间向量的坐标表示及应用 (1)数量积的坐标运算 设 a=(a1,a2,a3),b=(b1,b2,b3), 则 a·b= . 忆 一 忆 知 识 要 点λ(a·b) b·a a·b+a·c a1b1+a2b2+a3b3 要点梳理(2)共线与垂直的坐标表示 设 a=(a1,a2,a3),b=(b1,b2,b3), 则 a∥b⇔ ⇔ , , , a⊥b⇔ a·b=0⇔ (a,b 均为非零向量). (3)模、...