福建省建瓯市高一数学(基本不等式)课件VIP免费

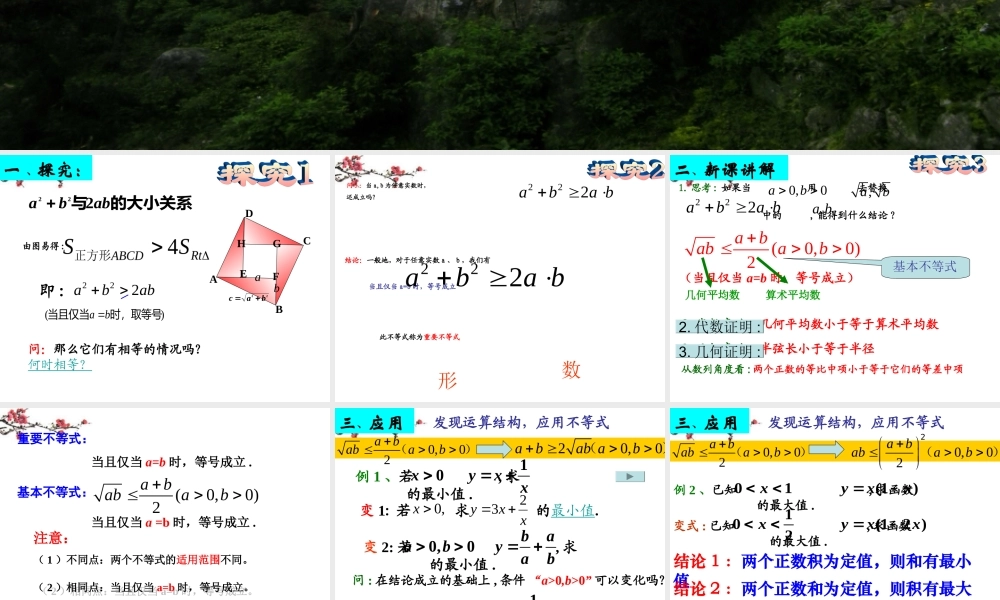
第 4 课时 基本不等式ADCBHGFE ab问：那么它们有相等的情况吗？何时相等？一 、探究：由图易得 :222abab即 :22bac)(时，取等号当且仅当ba 的大小关系与 abba222 结论：一般地，对于任意实数 a 、 b ，我们有 当且仅当 a=b 时，等号成立222aba b问 5 ：当 a,b 为任意实数时， 还成立吗？形数此不等式称为重要不等式222aba b2. 代数意义：几何平均数小于等于算术平均数2. 代数证明 :3. 几何意义：半弦长小于等于半径(0,0)2ababab（当且仅当 a=b 时，等号成立）二、新课讲解算术平均数几何平均数3. 几何证明 :从数列角度看 : 两个正数的等比中项小于等于它们的等差中项1. 思考 : 如果当 用 去替换 中的 , 能得到什么结论 ? 0,0ba,ab222aba bba,基本不等式基本不等式：当且仅当 a =b 时，等号成立 .当且仅当 a=b 时，等号成立 .222(abab aR、b）重要不等式：(0,0)2ababab注意：（ 1 ）不同点：两个不等式的适用范围不同。（ 2 ）相同点：当且仅当 a=b 时，等号成立。（ 2 ）相同点：当且仅当 a=b 时，等号成立。构造条件三、应用0,02ababab（）20,0abab ab（）例 1 、若 , 求 的最小值 .10 xyxx 变 3: 若 , 求 的最小值.13 3xyxx 变 2: 若 , 求 的最小值 .0,0 baabyab发现运算结构，应用不等式问 : 在结论成立的基础上 , 条件“ a>0,b>0” 可以变化吗？变 1: 若 求 的最小值.,0xxxy23 0,02ababab（）0,02ababab2（）三、应用例 2 、已知 , 求函数 的最大值 .01 (1)xyxx变式 : 已知 , 求函数 的最大值 .10 (12 )2xyxx发现运算结构，应用不等式应用要点：一正数 二定值 三相等结论 1 ：两个正数积为定值，则和有最小值结论 2 ：两个正数和为定值，则积有最大值3. 已知直角三角形的面积等于 50 ，两条直角边各为多少时 , 两条直角边的和最小，最小值是多少？4. 用 20cm 长的铁丝折成一个面积最大的矩形，应怎样折？ 四 、巩固.,,3,6,.2.,,,6,.1nmnmmnnmnmmnnmnm此时值有最则满足若正数此时值有最则满足若正数大933小262322100mxy例 3 ．用篱笆围一个面积为 的矩形菜园 , 问该矩形的长、宽各为多少时 , 所用篱笆最短，最短的篱笆是多少 ?2...