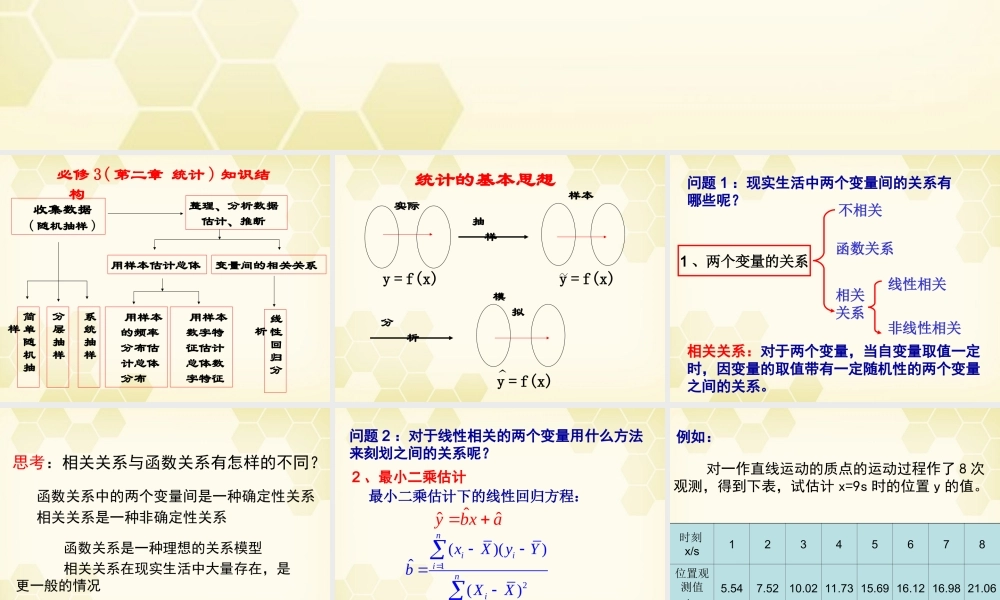
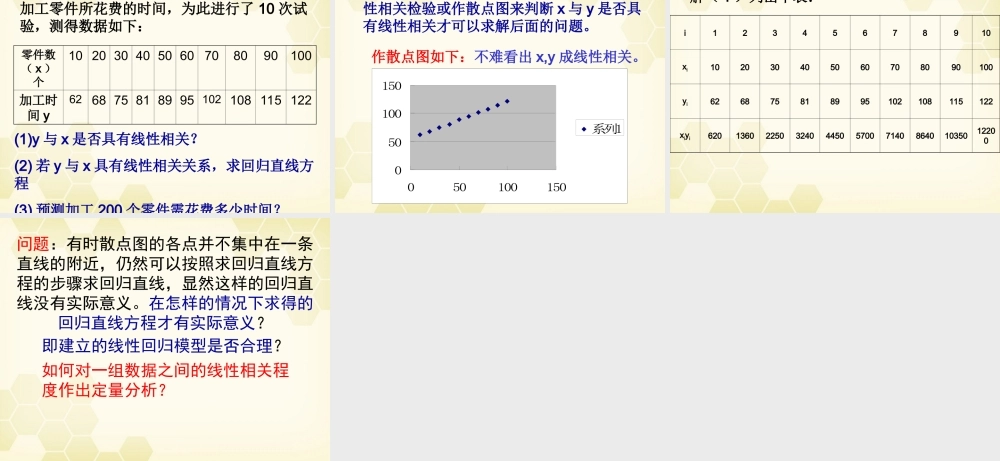
选修 1-2(一)必修 3( 第二章 统计 ) 知识结构 收集数据 ( 随机抽样 )整理、分析数据估计、推断简单随机抽样分层抽样系统抽样用样本估计总体变量间的相关关系 用样本的频率分布估计总体分布 用样本数字特征估计总体数字特征线性回归分析统计的基本思想y = f(x)y = f(x)y = f(x)实际样本模 拟抽 样分 析1 、两个变量的关系不相关相关关系函数关系线性相关非线性相关问题 1 :现实生活中两个变量间的关系有哪些呢?相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。思考:相关关系与函数关系有怎样的不同?函数关系中的两个变量间是一种确定性关系相关关系是一种非确定性关系 函数关系是一种理想的关系模型 相关关系在现实生活中大量存在,是更一般的情况问题 2 :对于线性相关的两个变量用什么方法来刻划之间的关系呢?2 、最小二乘估计最小二乘估计下的线性回归方程:ˆˆˆybxa121()()ˆ()niiiniixXyYbXXˆˆaYbX 对一作直线运动的质点的运动过程作了 8 次观测,得到下表,试估计 x=9s 时的位置 y 的值。时刻x/s12345678位置观测值y/cm5.547.5210.02 11.73 15.69 16.12 16.98 21.06例如:05101520250246810系列1i12345678xi12345678 4.50yi5.547.5210.0211.7315.6916.1216.9821.0613.08xiyi5.5415.0430.0646.9278.4596.72118.9168.5560.1xi214916253649642043 、回归分析的基本步骤 :画散点图求回归方程预报、决策数学3——统计1. 画散点图2. 求出 b,a 的值。3. 求回归直线方程4. 用回归直线方程解决应用问题4 、线性回归模型yabx 其中 a+bx 是确定性函数, 是随机误差注: 产生的主要原因: (1) 所用确定性函数不恰当; (2) 忽略了某些因素的影响; (3) 观测误差。思考:在时刻 x=9s 时,质点运动位置一定是 22.6287cm 吗?对于线性回归模型应注意以下两个问题:I 模型的合理性;II 在模型合理的情况下,如何估计 a,b.yabx 例 1. 下表给出我国从 1949 至 1999 年人口数据资料,试根据表中数据估计我国 2004 年的人口数。年份4954596469747984899499人口数 /百万5426036727058079099751035110711771246年份05101520253035404550人口数 /百万5426036727058079099751035110711771246分析:先画图例题 2. 一个车间为了规定工时定额,需要确定加工零件所花费的...