秋八年级数学上册 第5章 二次根式 5.3 二次根式的加法和减法教学课件 (新版)湘教版 课件VIP免费

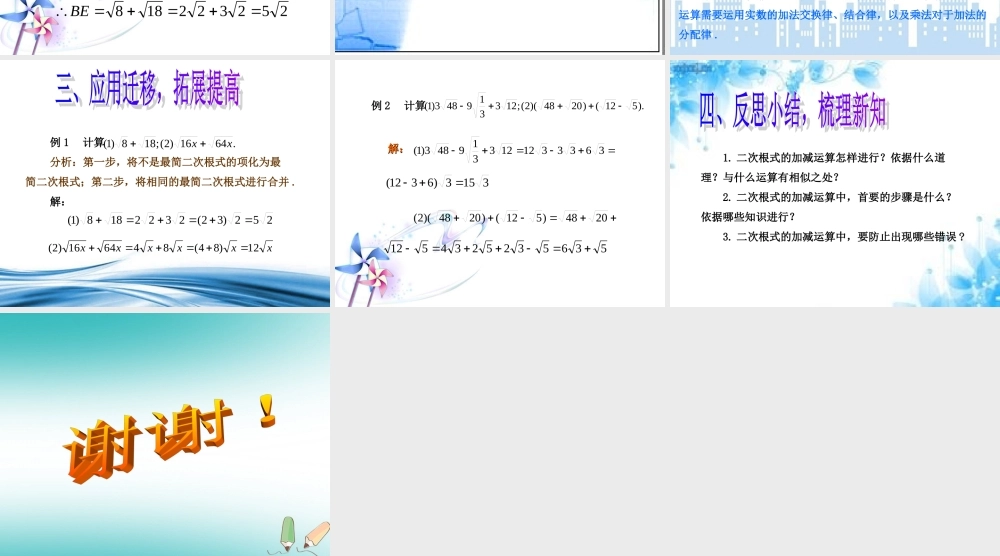
第五章 二次根式 5.3 二次根式的加法和减法 1. 使学生理解二次根式加减运算的基础，首要步骤是把各个二次根式化简，然后才加减 . 2. 使学生理解和掌握二次根式加减的法则：把被开方数相同的二次根式的系数相加减，被开方数不变 . 3. 使学生进行简单的二次根式的加、减运算 . 4. 通过观察、分析、联想、计算等活动，树立学生学好数学的自信心和培养学生概括、推理的能力 .重点：二次根式加减运算法则的形成与应用 .难点：化简二次根式，使之成为可加减的形式 . 1. 计算 2a2b+3ab2+a2b-4ab2, 并说明运算法则 . 2. 实数运算有哪些运算律？分配律用字母如何表示？ 引导学生完成教材 P167 的“动脑筋”，请学生思考以下问题： 问题问题 11 ：怎样算出：怎样算出 BEBE 的长？的长？ 分析： BE ＝ BC+CE ，即两个正方形的边长之和 . 正方形 ABCD 的面积为 8 ，其边长为 . 正方形 CEGH 的面积为 18 ，其边长为 ，252322188BE228 238  问题 2 ：你能用运算律说明的理由吗？ 因为实数的运算满足乘法对加法的分配律，所以上式成立 . 由此得出：被开方数相同的二次根式相加减，只要将系数相加减，被开方数不变 .252)32(2322 问题 3 ：你能算出 的结果吗？ 解： 可以看出，要将二次根式化简后才能进行加、减运算 . 综合上述结论，师生共同概括二次根式加减的步骤和方法：综合上述结论，师生共同概括二次根式加减的步骤和方法： （ 1 ）将算式中所有的二次根式化简； （ 2 ）将被开方数相同的二次根式的系数相加减，被开方数不变 . 联想：这类似于整式加减法的合并同类项，二次根式的加减运算需要运用实数的加法交换律、结合律，以及乘法对于加法的分配律 .383)53(353375277527  例 1 计算 分析：第一步，将不是最简二次根式的项化为最简二次根式；第二步，将相同的最简二次根式进行合并 . 解：xxxxxx12)84(846416)2(.6416)2(;188)1(xx 252)32(2322188)1( 例 2 计算53653252345122048)512()2048)(2().512()2048)(2(;123319483)1(3153)6312(3633312123319483)1(解：解： 1. 二次根式的加减运算怎样进行？依据什么道理？与什么运算有相似之处？ 2. 二次根式的加减运算中，首要的步骤是什么？依据哪些知识进行？ 3. 二次根式的加减运算中，要防止出现哪些错误 ?