高一数学三角函数模型的简单应用课件一 新课标 人教A版 课件VIP免费

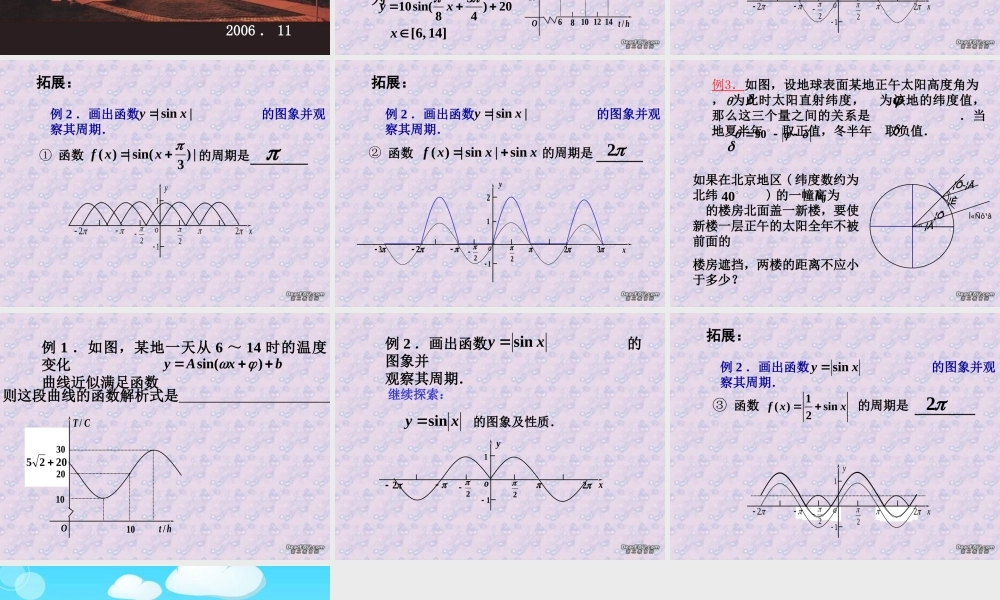
日期 2日46810 1214 161820 22 24 26 28 30潮高1.81.20.70.50.81.31.72.22.51.91.00.41.11.51.95.20.25.10.15.028142026o日期潮高 (m)xyo三角函数模型的简单应用（ 1 ）2006 ． 11例 1 ．如图，某地一天从 6 ～ 14 时的温度变化曲线近似满足函数（ 1 ）求这一天 6 ～ 14 时的最大温差；（ 2 ）写出这段曲线的函数解析式． bxAy)sin(OCT/ht /61014812102030（ 1 ）由图知，这段 时间的最大温差是解：Co20（ 2 ）所求解析式为20)438sin(10 xy]14,6[x例 2 ．画出函数 的图象并观察其周期． xyo222211yo222211x|sin|xy 拓展：例 2 ．画出函数 的图象并观察其周期． |sin|xy yo222211x|)3sin(|)(xxf函数的周期是①例 2 ．画出函数 的图象并观察其周期． |sin|xy 拓展：o2xxxfsin|sin|)(函数的周期是②213xy222132如果在北京地区 ( 纬度数约为北纬 ) 的一幢高为 的楼房北面盖一新楼，要使新楼一层正午的太阳全年不被前面的楼房遮挡，两楼的距离不应小于多少？ 例3．如图，设地球表面某地正午太阳高度角为 ， 为此时太阳直射纬度， 为该地的纬度值，那么这三个量之间的关系是 ．当地夏半年 取正值，冬半年 取负值．90¦È¦Õ¦Õ-¦Ä¦ÄÌ«Ñô¹â400hOCT/ht /101020302025例 1 ．如图，某地一天从 6 ～ 14 时的温度变化曲线近似满足函数 则这段曲线的函数解析式是 ． bxAy)sin(例 2 ．画出函数 的图象并观察其周期． xysin继续探索：xysin的图象及性质．yxo222211xxfsin21)(③ 函数的周期是例 2 ．画出函数 的图象并观察其周期． 拓展：xysinyo222211x2