高考数学复习(空间向量的应用(3))课件VIP免费

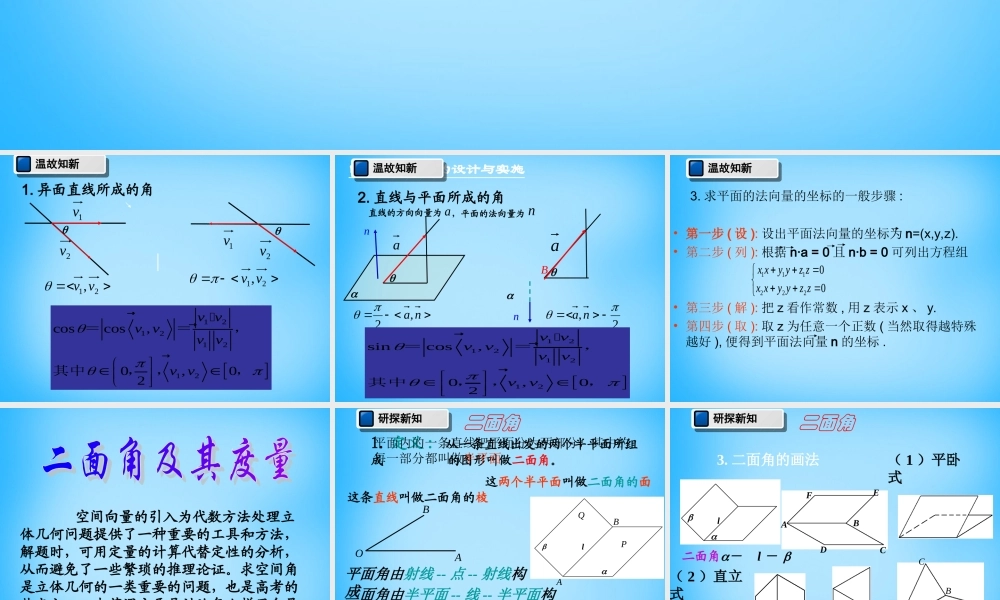
数学专题二温故知新1. 异面直线所成的角|1v2v21,vv2v1v21,vv12121212coscos,0,02v vv vvvv v����＝＝，其中，，，四、教学过程的设计与实施温故知新2. 直线与平面所成的角nBana,22,naanan直线的方向向量为，平面的法向量为 12121212sincos,0,02vvvvvvvv����＝＝，其中，，，3. 求平面的法向量的坐标的一般步骤 :• 第一步 ( 设 ): 设出平面法向量的坐标为 n=(x,y,z).• 第二步 ( 列 ): 根据 n·a = 0 且 n·b = 0 可列出方程组• 第三步 ( 解 ): 把 z 看作常数 , 用 z 表示 x 、 y.• 第四步 ( 取 ): 取 z 为任意一个正数 ( 当然取得越特殊越好 ), 便得到平面法向量 n 的坐标 . 11122200x xy yz zx xy yz z温故知新 空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法，解题时，可用定量的计算代替定性的分析，从而避免了一些繁琐的推理论证。求空间角是立体几何的一类重要的问题，也是高考的热点之一。本节课主要是讨论怎么样用向量的办法解决空间角之一 ---------- 问题。OBA1. 定义 : 从一条直线出发的两个半平面所组成 的图形叫做二面角。这条直线叫做二面角的棱这两个半平面叫做二面角的面平面角由射线 -- 点 -- 射线构成二面角由半平面 -- 线 -- 半平面构成2. 二面角的表示 : l二面角 AB二面角二面角lABPQPlQ二面角PABQ二面角平面内的一条直线把平面分为两部分，其中的每一部分都叫做半平面研探新知l二面角－ l － 二面角 C － AB － DABCD3. 二面角的画法CEFDAB（ 1 ）平卧式（ 2 ）直立式二面角研探新知思考： 4. 二面角的大小如何度量？ 以二面角的棱上任意一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。lO1BB1OAA1∠A O B∠A1O1B1二面角的大小用它的平面角来度量？显然与 O 的选取无关二面角研探新知注意：二面角的平面角必须满足：3 ）角的边都要垂直于二面角的棱1 ）角的顶点在棱上2 ）角的两边分别在两个面内10lOABAOB二面角研探新知本书约定：二面角的平面角的取值范围 是平面角是直角的二面角叫做直二面角[0, ]5. 二面角的取值范围如...