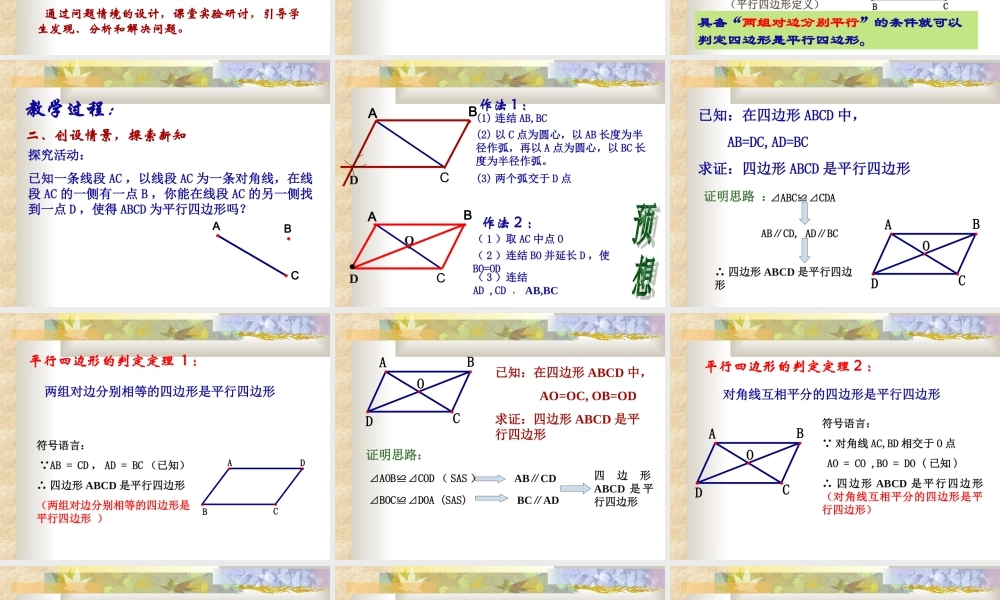
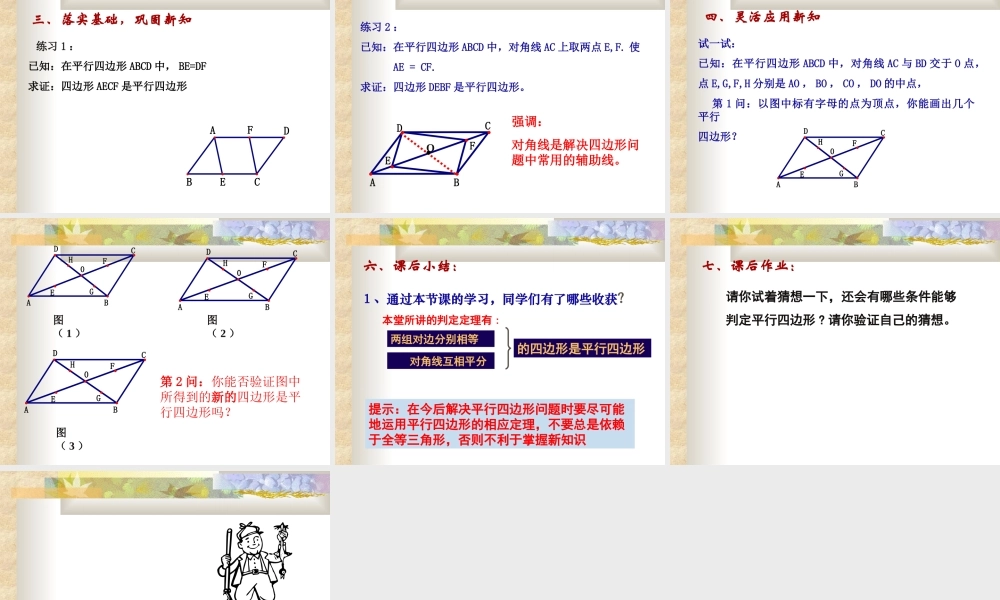
16.3.2 平行四边形的判定( 1 ) 教学目标:知识与技能: 掌握平行四边形判定定理 1 、 2 ,并会运用判定定理解决相关问题。 教学目标:过程与方法: 1 、经历对平行四边形判定方法的探究,使学生掌握并学会简单应用.2 、培养学生观察、分析、归纳的能力,养成勇于探索敢于创新的良好习惯,以及培养用数学方法分析、解决实际问题的能力,发展合情推理能力和说理能力。 教学目标:情感与态度: 学生通过观察、试验、类比、获得数学的猜想,体验数学活动充满着探索性和创造性,感受证明的必要性,证明过程的严谨性以及结论的准确性。发展学生克服困难的意志,通过一题多解激发学生的学习兴趣。 教学重点:掌握平行四边形的判定定理及其应用 教学难点:平行四边形判定定理的探究和归纳。 难点突破: 通过问题情境的设计,课堂实验研讨,引导学生发现、分析和解决问题。 教学方法: 合作探究式教学方法教学用具:多媒体辅助教学 教学过程:一、复习知识,导入新知 四边形 ABCD 具备怎样的条件就能判定它是平行四边形? BADC AB∥CD ,AD∥BC( 已知 ) ∴ 四边形 ABCD 是平行四边形 (平行四边形定义) 具备“两组对边分别平行”的条件就可以判定四边形是平行四边形。 二、创设情景,探索新知 教学过程:探究活动:已知一条线段 AC ,以线段 AC 为一条对角线,在线段 AC 的一侧有一点 B ,你能在线段 AC 的另一侧找到一点 D ,使得 ABCD 为平行四边形吗?ACB ACBD作法 1 :(1) 连结 AB,BC (2) 以 C 点为圆心,以 AB 长度为半径作弧,再以 A 点为圆心,以 BC 长度为半径作弧。(3) 两个弧交于 D 点 ACBDO作法 2 :( 1 )取 AC 中点 O( 2 )连结 BO 并延长 D ,使BO=OD ( 3 )连结AD ,CD , AB,BC ODACB已知:在四边形 ABCD 中, AB=DC,AD=BC求证:四边形 ABCD 是平行四边形 证明思路 :⊿ABC≌⊿CDA AB∥CD, AD∥BC ∴ 四边形 ABCD 是平行四边形 平行四边形的判定定理 1 :两组对边分别相等的四边形是平行四边形 BADC符号语言: AB = CD , AD = BC (已知)∴ 四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形 ) ODACB已知:在四边形 ABCD 中, AO=OC, OB=OD求证:四边形 ABCD 是平行四边形证明思路:⊿AOB≌⊿COD ( SAS ) ⊿BOC≌⊿DOA (SAS)AB∥CD BC∥AD 四边形ABCD 是 平行四...