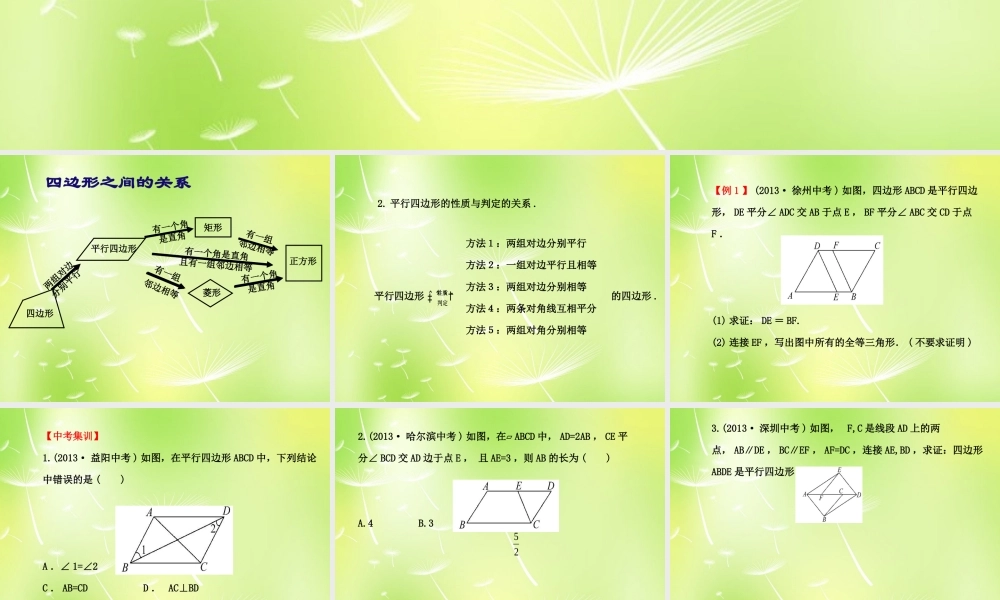
人教版八下总复习 平行四边形四边形之间的关系 四边形平行四边形矩形正方形两组对边分别平行有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等菱形菱形有一个角是直角且有一组邻边相等2. 平行四边形的性质与判定的关系 .平行四边形 ˆ ˆ ˆ†‡ ˆ ˆ ˆ性质判定方法1:两组对边分别平行方法2:一组对边平行且相等方法3:两组对边分别相等方法4:两条对角线互相平分方法5:两组对角分别相等的四边形 .【例 1 】 (2013· 徐州中考 ) 如图,四边形 ABCD 是平行四边形, DE 平分∠ ADC 交 AB 于点 E , BF 平分∠ ABC 交 CD 于点F .(1) 求证: DE = BF.(2) 连接 EF ,写出图中所有的全等三角形. ( 不要求证明 )【中考集训】1.(2013· 益阳中考 ) 如图,在平行四边形 ABCD 中,下列结论中错误的是 ( )A .∠ 1=∠2 B .∠ BAD=∠BCD C . AB=CD D . AC⊥BD2.(2013· 哈尔滨中考 ) 如图,在▱ ABCD 中, AD=2AB , CE 平分∠ BCD 交 AD 边于点 E , 且 AE=3 ,则 AB 的长为 ( )A.4 B.3 C. D.2523.(2013· 深圳中考 ) 如图, F,C 是线段 AD 上的两点, AB∥DE , BC∥EF , AF=DC ,连接 AE,BD ,求证:四边形ABDE 是平行四边形 .4.(2013· 日照中考 ) 如图,已知四边形 ABDE是平行四边形, C 为边 BD 延长线上一点,连接 AC,CE ,使 AB=AC.(1) 求证:△ BAD≌△ACE.(2) 若∠ B=30° ,∠ ADC=45° , BD=10 ,求平行四边形 ABDE的面积 .5.(2013· 重庆中考 ) 已知在▱ ABCD 中,AE⊥BC ,垂足为 E , CE=CD ,点 F 为 CE的中点,点 G 为 CD 上的一点,连接 DF ,EG , AG ,∠ 1=∠2 .(1) 若 CF=2 , AE=3 ,求 BE 的长 .(2) 求证:1CEGAGE.2 考点 2 特殊平行四边形的性质与判定【知识点睛】平行四边形、矩形、菱形、正方形性质的区别与联系1. 边:它们都具有对边平行且相等的性质,而菱形和正方形还具有四条边都相等的性质 .2. 角:它们都具有对角相等且邻角互补的性质,而矩形和正方形还具有四个角都是 90° 的性质 .3. 对角线:它们都具有对角线互相平分的性质,而矩形和正方形的对角线还具有相等的性质,菱形和正方形的对角线还具有互相垂直的性质 .【例 2 】 (2013· 雅安中考 ) 在▱ ABCD 中,点 E , F 分别在 AB,CD 上...