九年级数学下册 272 相似三角形的性质课件 (新版)新人教版 课件VIP免费

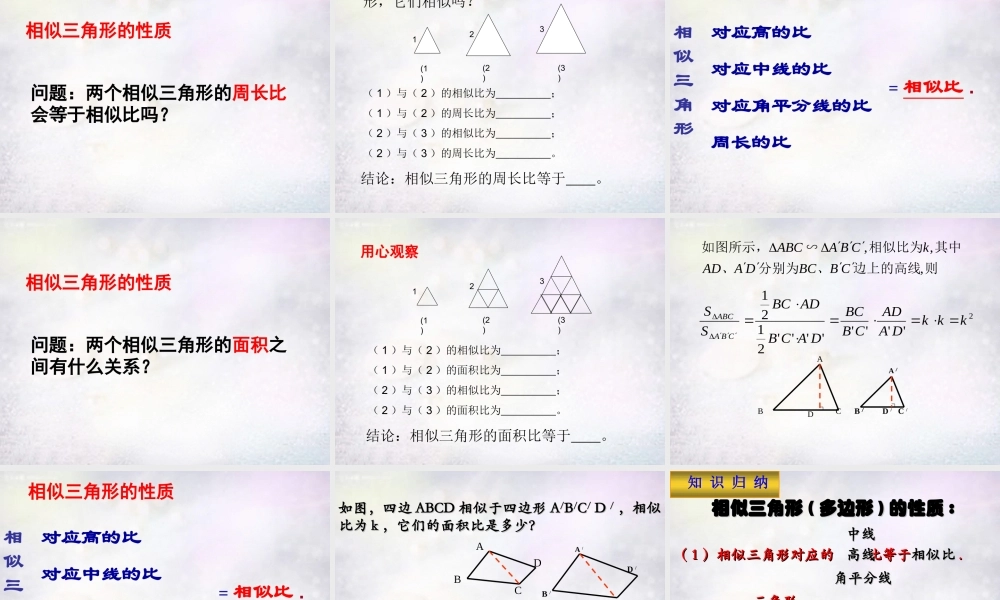
（ 2 ）相似三角形有什么性质？相似三角形对应角 ，相似三角形对应边 ；（ 1 ）相似三角形有哪些判定方法？温故知新想一想：它们还有哪些性质？一个三角形有三条重要线段：一个三角形有三条重要线段：情景引入高、中线、角平分线高、中线、角平分线如果两个三角形相似，那么这些对应线段有什么关系？如果两个三角形相似，那么这些对应线段有什么关系？ΔABC∽ΔAΔABC∽ΔA//BB//CC// ，，相似比为 相似比为 对应高的比 对应高的比 观察21DAADABDC A/B/C/D/21ΔABC∽ΔAΔABC∽ΔA//BB//CC// ，，相似比为 相似比为 对应中线的比 对应中线的比 观察21DAADABDCA/B/C/D/21ΔABC∽ΔAΔABC∽ΔA//BB//CC// ，，相似比为 相似比为 对应角平分线的比 对应角平分线的比 观察21DAADABDCA/B/C/D/21可得：对应高的比 可得：对应高的比 对应中线的比对应中线的比 对应角平分线的比对应角平分线的比小结当当 ΔABC∽ΔAΔABC∽ΔA//BB//CC// ，且相似比为 时，且相似比为 时 21DAADDAADDAAD观察这些数据，你会有怎样的猜想呢？观察这些数据，你会有怎样的猜想呢？ 212121ABCDA /B /C /D /①① 相似三角形的对应高相似三角形的对应高线之比等于相似比。线之比等于相似比。探索新知相似三角形的性质kDAADCBBC、DAAD、kCBAABC:,,1求证：边上的高线分别为其中相似比为∽：如图所示，问题kBAABDAADDBAABDCBAABC∽∽解：.90BDAADB又B'B自主思考 -- 类似结论DAADCBBC、DAAD、kCBAABC则边上的中线分别为其中相似比为∽：如图问题,,,2BDCAB′D′C′A′ 相似三角形的对应中线之比等于相似比。相似三角形的对应中线之比等于相似比。K自主思考 -- 类似结论 相似三角形的对应角平线之比等于相似比。相似三角形的对应角平线之比等于相似比。'',',,3DAADAA、DAAD、kCBAABC则的平分线分别为其中相似比为∽：问题BDCAB′D′C′A′K对应高的比对应中线的比对应角平分线的比 相似三角形相似三角形的性质相似比=相似三角形对应线段的比等于在相似三角形中还有哪些线段的比等于相似比？相似比11 、相似三角形对应边的比为、相似三角形对应边的比为 2:32:3 ，那么相似比，那么相似比为为 ，，对应角的角平分线的比为 。。 22 、两个相似三角...