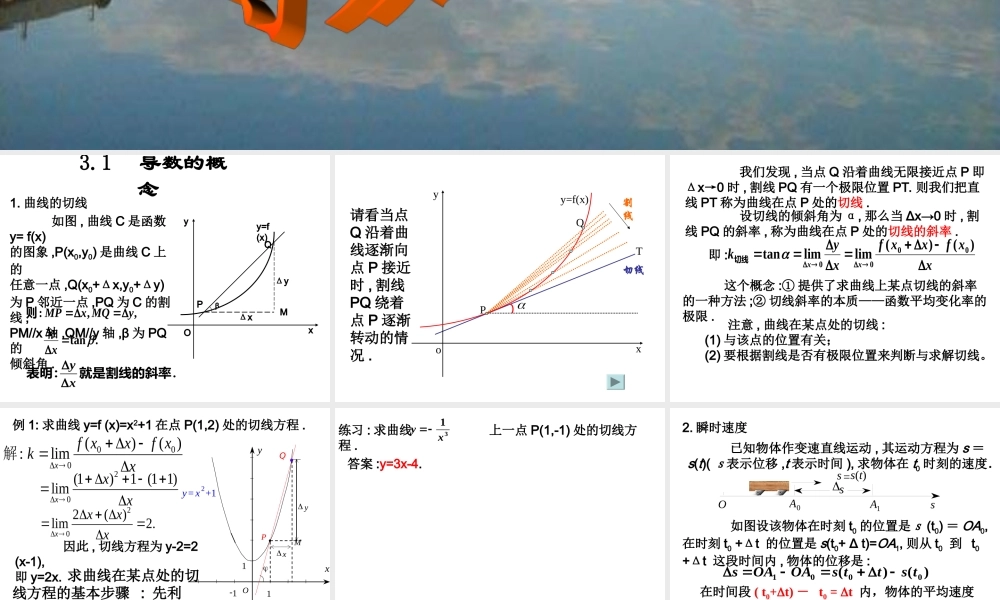
3.1 导数的概念 1. 曲线的切线βy=f(x)PQMΔxΔyOxyβPy=f(x)QMΔxΔyOxy 如图 , 曲线 C 是函数y= f(x)的图象 ,P(x0,y0) 是曲线 C 上的任意一点 ,Q(x0+Δx,y0+Δy)为 P 邻近一点 ,PQ 为 C 的割线 ,PM//x 轴 ,QM//y 轴 ,β 为 PQ的倾斜角 ..tan,,:xyyMQxMP则.就是割线的斜率表明: xy PQoxyy=f(x)割线切线T 请看当点Q 沿着曲线逐渐向点 P 接近时 , 割线PQ 绕着点 P 逐渐转动的情况 . 我们发现 , 当点 Q 沿着曲线无限接近点 P 即Δx→0 时 , 割线 PQ 有一个极限位置 PT. 则我们把直线 PT 称为曲线在点 P 处的切线 . 设切线的倾斜角为 α, 那么当 Δx→0 时 , 割线 PQ 的斜率 , 称为曲线在点 P 处的切线的斜率 .即 :xxfxxfxykxx)()(limlimtan0000切线 这个概念 :① 提供了求曲线上某点切线的斜率的一种方法 ;② 切线斜率的本质——函数平均变化率的极限 . 注意 , 曲线在某点处的切线 : (1) 与该点的位置有关; (2) 要根据割线是否有极限位置来判断与求解切线。 例 1: 求曲线 y=f (x)=x2+1 在点 P(1,2) 处的切线方程 .QPy= x 2+1xy-111OM yx000()():limxf xxf xkx 解 因此 , 切线方程为 y-2=2(x-1),即 y=2x. 求曲线在某点处的切线方程的基本步骤 : 先利用切线斜率的定义求出切线的斜率 , 然后利用点斜式求切线方程 .20(1)1 (1 1)limxxx 202()lim2.xxxx 练习 : 求曲线 上一点 P(1,-1) 处的切线方程 .31xy答案 :y=3x-4. 2. 瞬时速度 已知物体作变速直线运动 , 其运动方程为 s =s(t)( s表示位移 ,t 表示时间 ), 求物体在 t0 时刻的速度.O A 0 A 1 s s s(t) s = 如图设该物体在时刻 t0 的位置是s (t0) = OA0,在时刻 t0 +Δt 的位置是 s(t0+ Δ t)=OA1, 则从 t0 到 t0 +Δt 这段时间内 , 物体的位移是 :在时间段 ( t0+t) - t0 = t 内,物体的平均速度为 :tsttttsttsv0000__)()()()()(0001tsttsOAOAs 平均速度反映了物体运动时的快慢程度 , 但要精确地描述非匀速直线运动 , 就要知道物体在每一时刻运动的快慢程度 , 也既需要通过瞬时速度来反映 . 如果物体的运动规律是 s=s(t) ,...