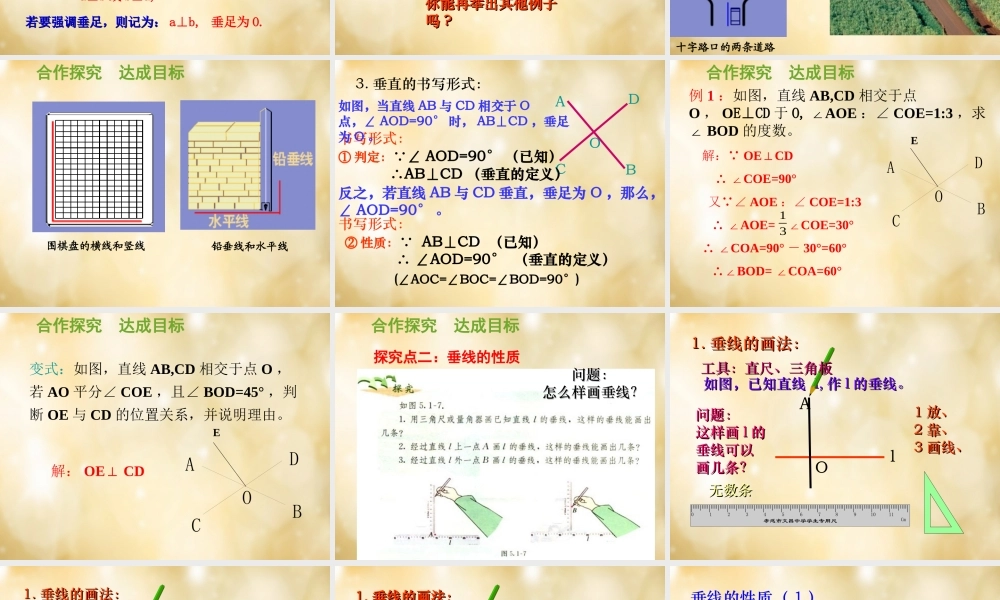
在相交线的模型中 , 固定木条 a, 转动木条 b,当 α =90° 时 ,a 与 b 垂直 .当 b 的位置变化时 ,a 、 b 所成的角 α 也会发生变化 .当 α ≠90° 时 ,a 与 b不垂直,叫斜交 .两条直线相交斜交垂直 垂直是相交的特殊情况)α α aabbbbbbbbbb)α α 创设情景 明确目标13理解垂线的定义;会过一点画已知直线的垂线。学 习 目 标2掌握垂线的性质并会应用;合作探究 达成目标探究点一:垂线的概念阅读教材第 3 页至 4 页,思考下列问题:1.两条相交直线在什么情况下是垂直的? 什么叫垂线?什么叫垂足?2. 垂线是一条直线还是线段 ?3. 请举出生活中垂直的例子。1. 垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”和直线字母表示垂直用“⊥”和直线字母表示垂直Oα 2.2. 垂直的表示:垂直的表示:例如、如图,例如、如图, aa 、、 bb 互相垂直互相垂直 , , 垂足为垂足为 OO ,则,则记为:记为:a⊥b 或 b⊥a, 若要强调垂足,则记为:若要强调垂足,则记为: a⊥b, 垂足为 O.合作探究 达成目标合作探究 达成目标日常生活中日常生活中 ,, 两条直线互相垂直的情形很常两条直线互相垂直的情形很常见见 ,, 说出图说出图 5.1-65.1-6 中的一些互相垂直的线中的一些互相垂直的线条条 ..你能再举出其他例子你能再举出其他例子吗吗 ??十字路口的两条道路围棋盘的横线和竖线铅垂线和水平线合作探究 达成目标ABCDO书写形式:如图,当直线 AB 与 CD 相交于 O点,∠ AOD=90° 时, AB⊥CD ,垂足为 O 。① 判定: ∠ AOD=90° (已知) ∴AB⊥CD (垂直的定义)书写形式:反之,若直线 AB 与 CD 垂直,垂足为 O ,那么,∠ AOD=90° 。② 性质: AB⊥CD (已知) ∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)3. 垂直的书写形式:合作探究 达成目标ODCBAE例 1 :如图,直线 AB,CD 相交于点O , OE⊥CD 于 O, AOE∠:∠ COE=1:3 ,求∠ BOD 的度数。解: OECD⊥ ∴ ∠COE=90° 又 ∠ AOE :∠ COE=1:3 ∴ ∠AOE= COE=30°∠ ∴ ∠COA=90° - 30°=60° ∴∠BOD= COA=60°∠31 合作探究 达成目标ODCBAE变式:如图,直线 AB,CD 相交于点 O ,若 AO 平分∠ COE ,且∠ BOD=45° ,判断 OE ...