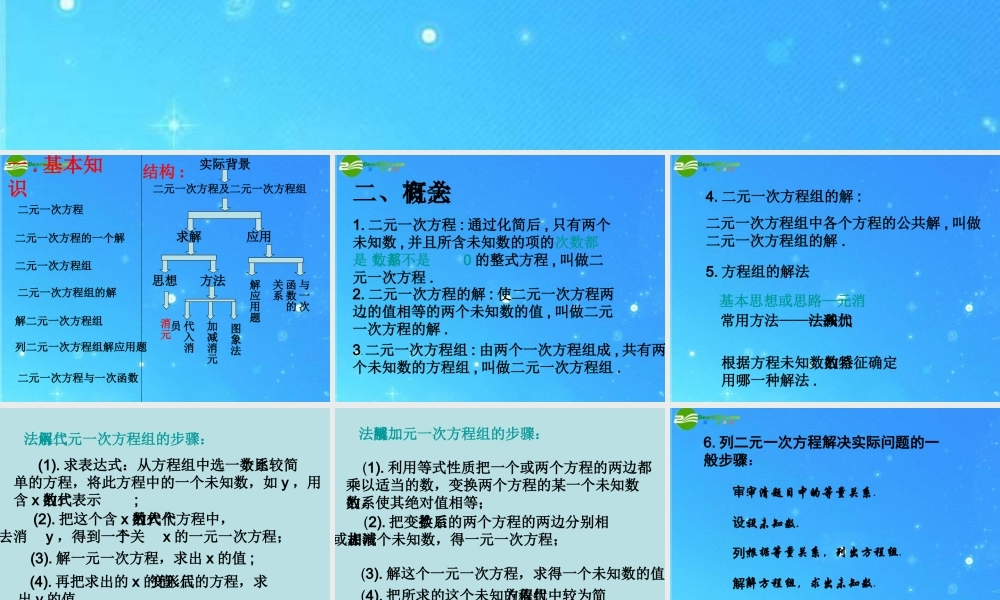
一 . 基本知识二元一次方程二元一次方程的一个解二元一次方程组二元一次方程组的解解二元一次方程组结构 :实际背景二元一次方程及二元一次方程组求解应用方法思想列二元一次方程组解应用题二元一次方程与一次函数解应用题与一次函数的关系消元代入消员加减消元图象法 二、有关概念1. 二元一次方程 : 通过化简后 , 只有两个未知数 , 并且所含未知数的项的次数都是 1, 系数都不是0 的整式方程 , 叫做二元一次方程 .2. 二元一次方程的解 : 使二元一次方程两边的值相等的两个未知数的值 , 叫做二元一次方程的解 .3.二元一次方程组 : 由两个一次方程组成 , 共有两个未知数的方程组 , 叫做二元一次方程组 . 4. 二元一次方程组的解 :二元一次方程组中各个方程的公共解 , 叫做二元一次方程组的解 .5. 方程组的解法根据方程未知数的系数特征确定用哪一种解法 .基本思想或思路——消元常用方法————代入法和加减法用代入法解二元一次方程组的步骤: (1). 求表达式:从方程组中选一个系数比较简单的方程,将此方程中的一个未知数,如 y ,用含 x 的代数式表示; (2). 把这个含 x 的代数式代入另一个方程中,消去y ,得到一个关于x 的一元一次方程; (3). 解一元一次方程,求出 x 的值 ; (4). 再把求出的 x 的值 代入变形后的方程,求出 y 的值 .用加减法解二元一次方程组的步骤: (1). 利用等式性质把一个或两个方程的两边都乘以适当的数,变换两个方程的某一个未知数的系数,使其绝对值相等; (2). 把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程; (3). 解这个一元一次方程,求得一个未知数的值 ; (4). 把所求的这个未知的值代入方程组中较为简便的一个方程,求出另一个未知数,从而得到方程的解 . 6. 列二元一次方程解决实际问题的一般步骤: 审: 设: 列: 解: 答:审清题目中的等量关系. 设未知数. 根据等量关系,列出方程组. 解方程组,求出未知数. 检验所求出未知数是否符合题意,写出答案. 二元一次方程组和一次函数的图象的关系方程组的解是对应的两条直线的交点坐标两条线的交点坐标是对应的方程组的解二元一次方程和一次函数的图象的关系以二元一次方程的解为坐标的点都在对应的函数图象上 .一次函数图象上的点的坐标都适合对应的二元一次方程 . 1. 已知方程组 的解是 则 , .2. 已知代数式 , 当 时,...