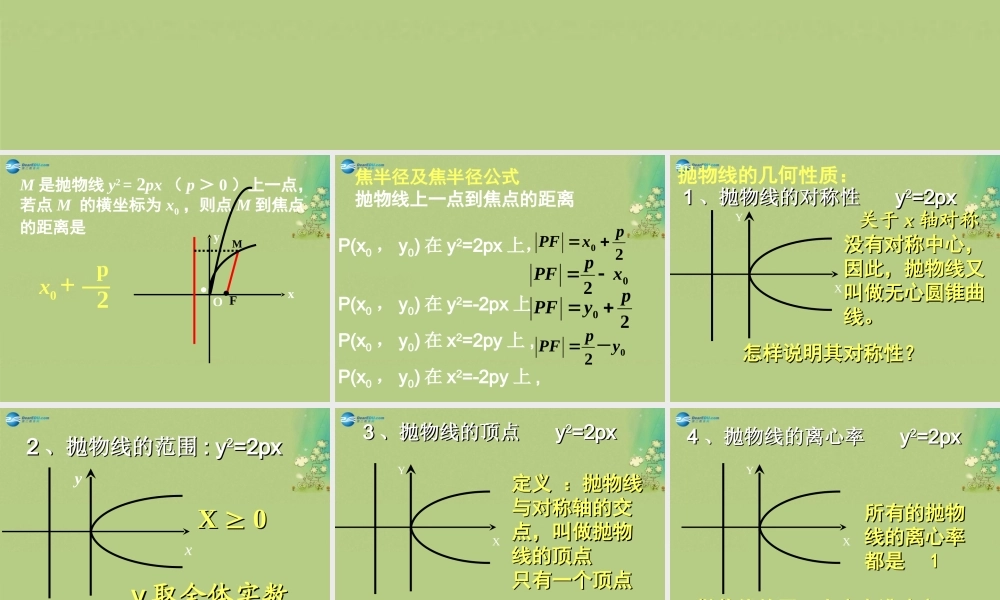
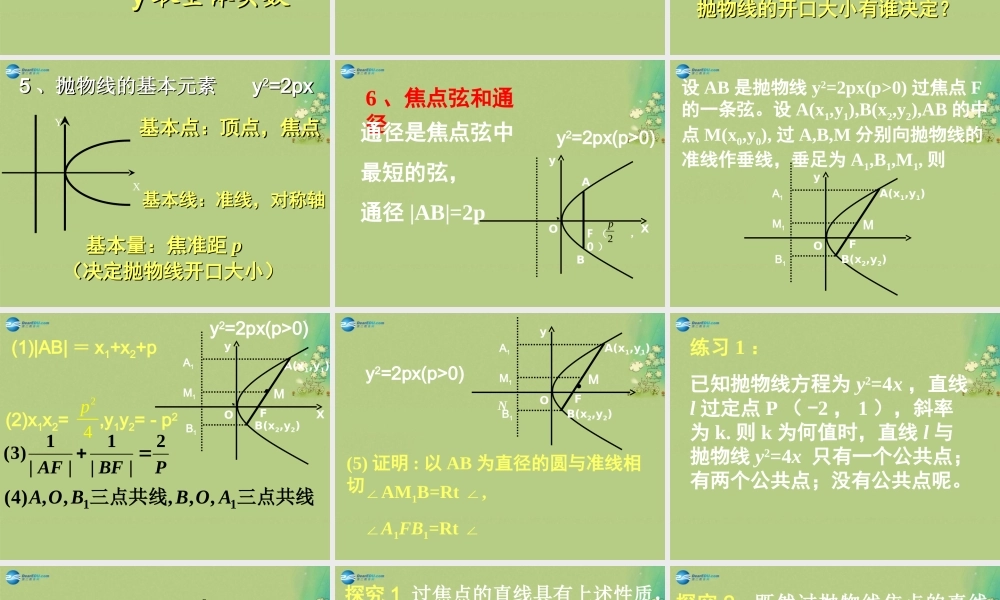
2.2.22.2.2抛物线的简单性质抛物线的简单性质M 是抛物线 y2 = 2px ( p > 0 )上一点,若点 M 的横坐标为 x0 ,则点 M 到焦点的距离是x0 + —2pOyx.FM.焦半径及焦半径公式抛物线上一点到焦点的距离P(x0 , y0) 在 y2=2px 上, P(x0 , y0) 在 y2=-2px 上 ,P(x0 , y0) 在 x2=2py 上 ,P(x0 , y0) 在 x2=-2py 上 ,20pxPF02xpPF20pyPF02ypPF-11 、抛物线的对称性 、抛物线的对称性 yy22=2px=2px关于关于 xx 轴对称轴对称没有对称中心,没有对称中心,因此,抛物线又因此,抛物线又叫做无心圆锥曲叫做无心圆锥曲线。线。XY怎样说明其对称性?怎样说明其对称性?抛物线的几何性质:22 、抛物线的范围、抛物线的范围 : y: y22=2px=2pxyy 取全体实数取全体实数xyX X 0 0定义 :抛物线定义 :抛物线与对称轴的交与对称轴的交点,叫做抛物点,叫做抛物线的顶点线的顶点只有一个顶点只有一个顶点 XY33 、抛物线的顶点 、抛物线的顶点 yy22=2px=2px所有的抛物所有的抛物线的离心率线的离心率都是 都是 11XY44 、抛物线的离心率 、抛物线的离心率 yy22=2px=2px抛物线的开口大小有谁决定?抛物线的开口大小有谁决定?基本点:顶点,焦点基本点:顶点,焦点基本线:准线,对称轴基本线:准线,对称轴基本量:焦准距基本量:焦准距 ppXY55 、抛物线的基本元素 、抛物线的基本元素 yy22=2px=2px(决定抛物线开口大小)(决定抛物线开口大小) 6 、焦点弦和通径通径是焦点弦中最短的弦,通径 |AB|=2pXyF ( ,0 )OBy2=2px(p>0)A2p设 AB 是抛物线 y2=2px(p>0) 过焦点 F的一条弦。设 A(x1,y1),B(x2,y2),AB 的中点 M(x0,y0), 过 A,B,M 分别向抛物线的准线作垂线,垂足为 A1,B1,M1, 则yFA(x1,y1)OB(x2,y2)MA1B1M1A(x1,y1)(1)|AB| = x1+x2+p (2)x1x2= ,y1y2= - p224pPBFAF2||1||1)3(XyFOB(x2,y2)MA1B1M1y2=2px(p>0)三点共线三点共线11,,,,,)4(AOBBOAyFA(x1,y1)OB(x2,y2)MA1B1M1(5) 证明 : 以 AB 为直径的圆与准线相切y2=2px(p>0)∠AM1B=Rt , ∠∠A1FB1=Rt ∠N练习 1 :已知抛物线方程为 y2=4x ,直线l 过定点 P ( -2 , 1 ),斜率为 k. 则 k 为何值时,直线 l 与抛物线 y2=4x 只有一个公共点;有两个公共点;没有公共点呢。提出问题 过抛物线 的焦点的一条直线和抛物线相交,两交点的纵坐标为 .求证: ...