八年级数学乘法公式课件1华师版 课件VIP免费

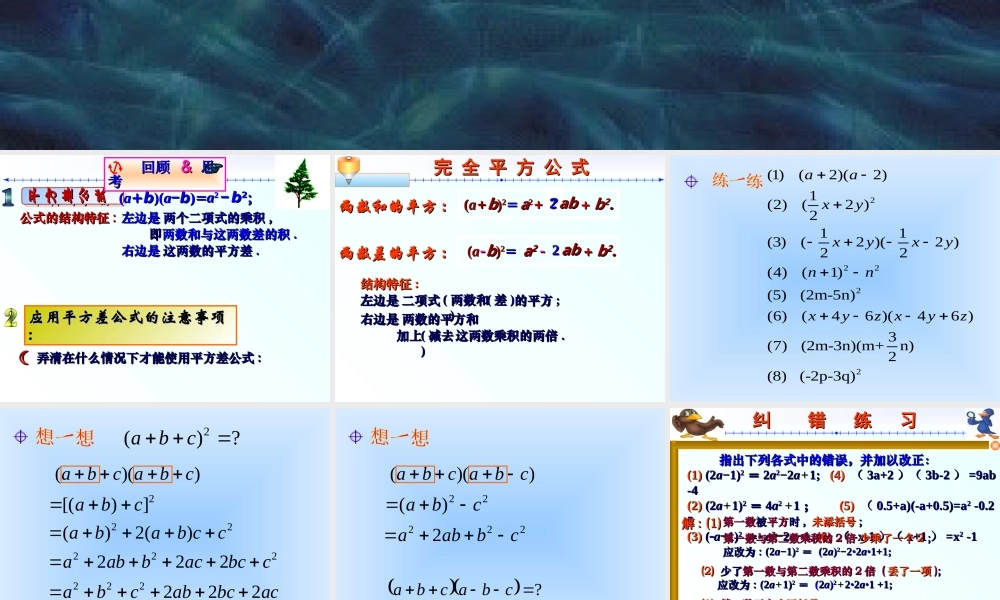
标题标题标题标题回顾与思考公式的结构特征公式的结构特征 :: 左边是左边是aa2 2 −− bb22;; 两个二项式的乘积两个二项式的乘积 ,,平方差公式平方差公式平方差公式平方差公式应用平方差公式的注意事项应用平方差公式的注意事项:: 回顾 回顾 && 思思考考☞☞((aa++bb)()(aa−−bb))==即即两数和与这两数差的积两数和与这两数差的积 ..右边是右边是 这两数的平方差这两数的平方差 ..☾☾ 弄清在什么情况下才能使用平方差公式弄清在什么情况下才能使用平方差公式 :: 完 全 平 方 公 式完 全 平 方 公 式((aa++bb))22== aa22++aabb ++ bb22..22两数和的平方两数和的平方 ::两数差的平方两数差的平方 ::((aa--bb))22== aa2 2 --aabb ++ bb22..22结构特征结构特征 ::左边是左边是的平方的平方 ;;二项式二项式右边是右边是(( 两数和 两数和 ))(( 差差 ))两数的平方和两数的平方和加上加上(( 减去减去))这两数乘积的两倍这两数乘积的两倍 .. 22222(1) (2)(2)1(2) (2 )211(3) (2 )(2 )22(4) (1)(5) (2m-5n)(6) (46 )(46 )3(7) (2m-3n)(m+n)2(8) (-2p-3q)aaxyxyxynnxyzxyz ()()abc abc  2[()]abc22()2()abab cc2()?abc 222222222222aabbacbccabcabbcac ))((cbacba22)(cba2222cbaba?cbacba纠 错 练 习纠 错 练 习 指出下列各式中的错误，并加以改正：指出下列各式中的错误，并加以改正：(1)(1) (2(2aa−1)−1)22 ＝＝ 22aa22−2−2aa++1; 1; (4)(4) （（ 3a+23a+2 ）（）（ 3b-23b-2 ）） =9ab=9ab-4-4(2)(2) (2 (2aa++1)1)22 ＝＝ 44aa2 2 ++11 ； ； (5)(5) （（ 0.5+a)(-a+0.5)=a0.5+a)(-a+0.5)=a22 -0.2 -0.255(3) (3) ((aa−−1)1)22 ＝＝ aa22−−22aa−−1. 1. (6) (6) （（ -x-1-x-1 ）（）（ x+1x+1 ）） =x=x22 -1 -1解解 : (1): (1) 第一数第一数被被平方平方时时 , , 未添括号未添括号 ;;第一数与第二数乘积的第一数与第二数乘积的 22 倍 倍 少乘了一个少乘了一个 22 ; ;应改为应改为 : : (2(2aa−1)−1)22 ＝ ＝ ((22aa))22−2−2••22aa••1+1;1+1; (2)(2) 少了少了第一数与第二数乘积的第一数与第二数乘积的 22 倍 倍 (( 丢了一项丢了一项 ));;应改为...