九年级数学下课件二次函数的图象和性质 课件VIP免费

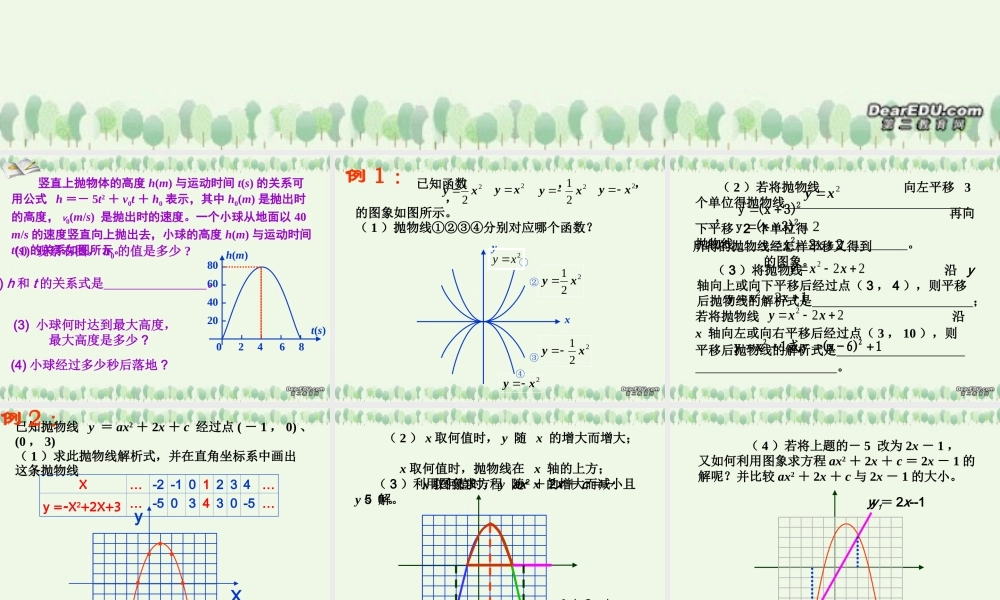
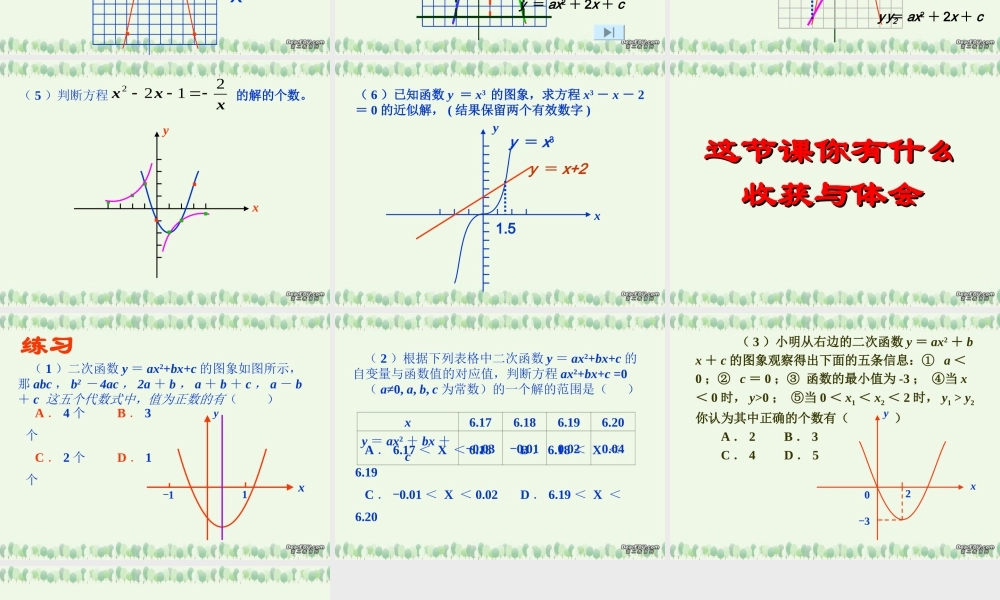
二次函数的图象和性质(1) 观察右图， h0 的值是多少 ? 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可用公式 h ＝－ 5t2 ＋ v0t ＋ h0 表示，其中 h0(m) 是抛出时的高度， v0(m/s) 是抛出时的速度。一个小球从地面以 40m/s 的速度竖直向上抛出去，小球的高度 h(m) 与运动时间t(s) 的关系如图所示。(3) 小球何时达到最大高度， 最大高度是多少 ?0 2 4 6 880604020t(s)h(m)(2) h 和 t 的关系式是 。(4) 小球经过多少秒后落地 ?例 1 ： 已知函数 ， ， ，的图象如图所示。 （ 1 ）抛物线①②③④分别对应哪个函数？221 xy 2xy 221 xy2xyxy①②③④2xy 221 xy 221 xy2xy （ 2 ）若将抛物线 向左平移 3个单位得抛物线 ，2xy 22xxy2 所得的抛物线经怎样平移又得到 的图象。 再向下平移 2 个单位得抛物线 。222xxy若将抛物线 沿 x 轴向左或向右平移后经过点（ 3 ， 10 ），则平移后抛物线的解析式是 。 （ 3 ）将抛物线 沿 y 轴向上或向下平移后经过点（ 3 ， 4 ），则平移后抛物线的解析式是 ；222xxy23)(xy223)(xy1xxy2216)-(x1或yxy22已知抛物线 y ＝ ax2 ＋ 2x ＋ c 经过点 ( － 1 ， 0) 、(0 ， 3)（ 1 ）求此抛物线解析式，并在直角坐标系中画出这条抛物线例 2 ：·· ···Xy··X… -2 -1 0 1 2 3 4…y =-X2+2X+3 … -5 03 4 3 0 -5 … （ 2 ） x 取何值时， y 随 x 的增大而增大； x 取何值时，抛物线在 x 轴的上方； x 取何值时， y 随 x 的增大而减小且 y < ０。y ＝ ax2 ＋ 2x ＋ c （ 3 ）利用图象求方程 ax2 ＋ 2x ＋ c ＝－5 解。 （ 4 ）若将上题的－ 5 改为 2x － 1 ， 又如何利用图象求方程 ax2 ＋ 2x ＋ c ＝ 2x － 1 的解呢？并比较 ax2 ＋ 2x ＋ c 与 2x － 1 的大小。y ＝ ax2 ＋ 2x ＋ cy ＝ 2x--1y1 y2 xy····（ 5 ）判断方程的解的个数。 xxx2122·······（ 6 ）已知函数 y ＝ x3 的图象，求方程 x3 － x － 2＝ 0 的近似解， ( 结果保留两个有效数字 ) xy1.5y ＝ x3y ＝ x+2这节课你有什么这节课你有什么收获与体会收获与体会（ 1 ）二次函数 y ＝ ax2+bx+c 的图象如图所示，那...