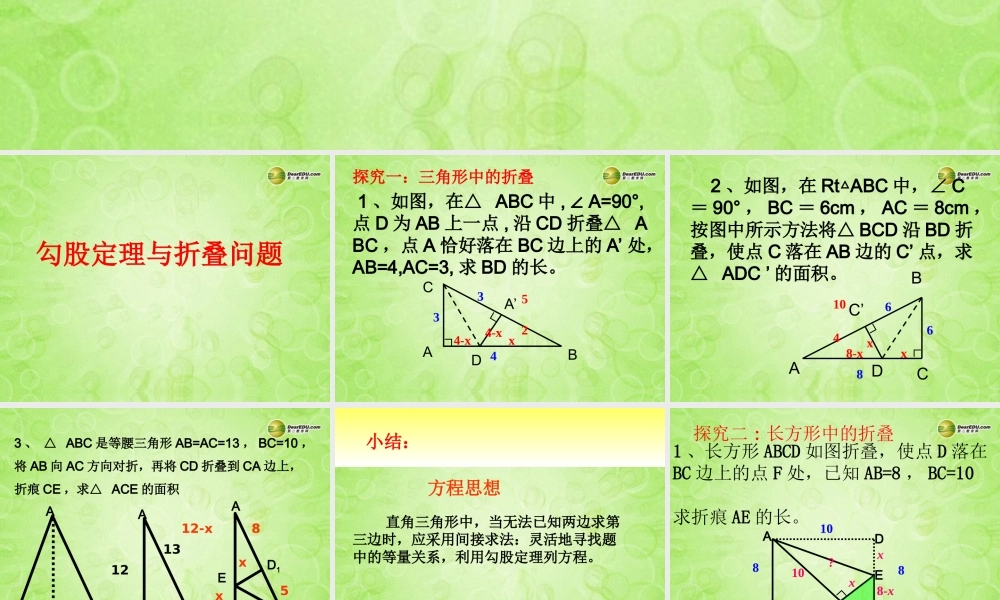
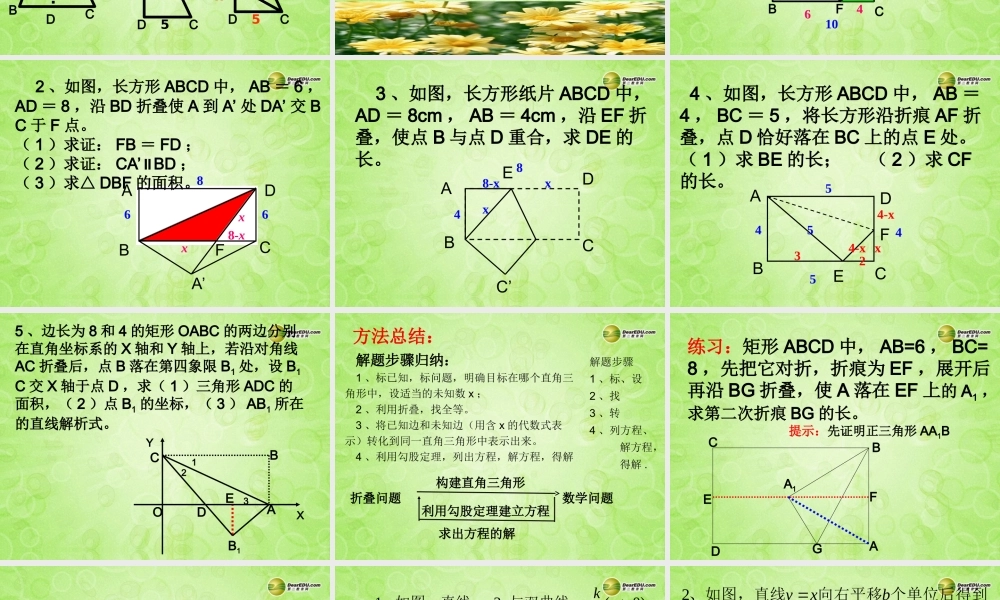
勾股定理专题复习勾股定理与折叠问题 及勾股定理与反比例函数勾股定理与折叠问题 1 、如图,在△ ABC 中 , A=90°,∠点 D 为 AB 上一点 , 沿 CD 折叠△ ABC ,点 A 恰好落在 BC 边上的 A’ 处,AB=4,AC=3, 求 BD 的长。探究一:三角形中的折叠CABDA’∟∟x433524-x4-x 2 、如图,在 Rt ABC△中,∠ C= 90° , BC = 6cm , AC = 8cm ,按图中所示方法将△ BCD 沿 BD 折叠,使点 C 落在 AB 边的 C’ 点,求△ ADC ’ 的面积。AC’DCB∟∟686104xx8-x3 、 △ ABC 是等腰三角形 AB=AC=13 , BC=10 ,将 AB 向 AC 方向对折,再将 CD 折叠到 CA 边上,折痕 CE ,求△ ACE 的面积ABCDADCDCAD1E13512512-x5xx8 方程思想 直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。小结:ABCDFE810810106xx8-x4?探究二 : 长方形中的折叠1 、长方形 ABCD 如图折叠,使点 D 落在BC 边上的点 F 处,已知 AB=8 , BC=10,求折痕 AE 的长。∟ 2 、如图,长方形 ABCD 中, AB = 6 ,AD = 8 ,沿 BD 折叠使 A 到 A’ 处 DA’ 交 BC 于 F 点。( 1 )求证: FB = FD ;( 2 )求证: CA’ BD∥;( 3 )求△ DBF 的面积。ABCA’DF68xx68-x 3 、如图,长方形纸片 ABCD 中,AD = 8cm , AB = 4cm ,沿 EF 折叠,使点 B 与点 D 重合,求 DE 的长。AEDBC’C84x8-xx 4 、如图,长方形 ABCD 中, AB =4 , BC = 5 ,将长方形沿折痕 AF 折叠,点 D 恰好落在 BC 上的点 E 处。( 1 )求 BE 的长; ( 2 )求 CF的长。AFBECD455532x4-x4-x45 、边长为 8 和 4 的矩形 OABC 的两边分别在直角坐标系的 X 轴和 Y 轴上,若沿对角线AC 折叠后,点 B 落在第四象限 B1 处,设 B1C 交 X 轴于点 D ,求( 1 )三角形 ADC 的面积,( 2 )点 B1 的坐标,( 3 ) AB1 所在的直线解析式。123EOCBAB1DXY折叠问题利用勾股定理建立方程数学问题求出方程的解构建直角三角形方法总结:解题步骤归纳:1 、标已知,标问题,明确目标在哪个直角三角形中,设适当的未知数 x ;2 、利用折叠,找全等。3 、将已知边和未知边(用含 x 的代数式表示)转化到同一直角三角形中表示出来。4 、利用勾股定理,列出方...