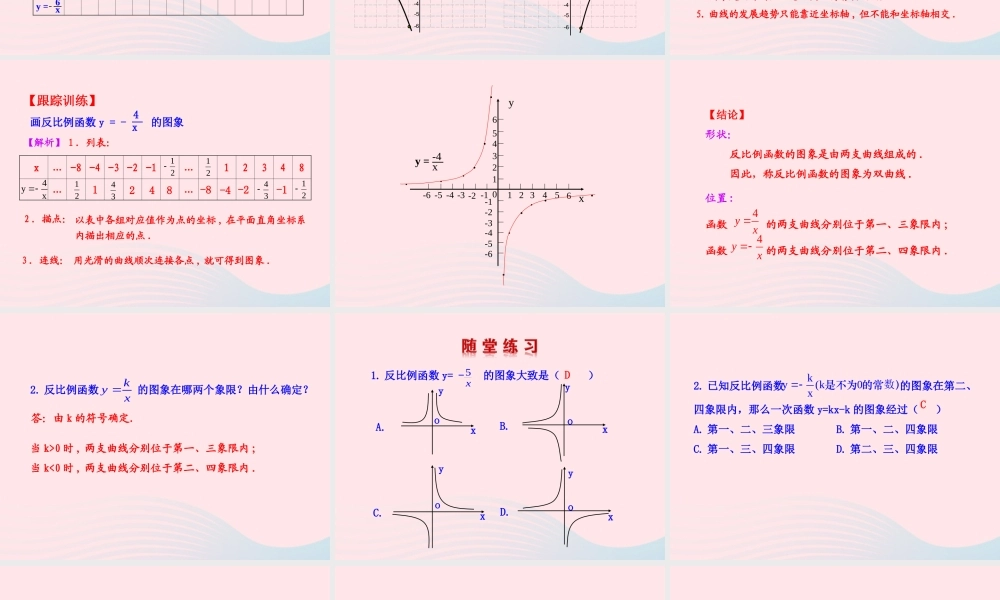
1.2 反比例函数的图象与性质第 1 课时1. 进一步熟悉作函数图象的步骤,会画反比例函数的图象;2. 体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力,探索并掌握反比例函数的主要性质.1. 什么是反比例函数?2. 在反比例函数的定义中需要注意什么?( 1 ) k 是非零常数 .( 2 ) xy = k .一般地,形如 y = ( k 是常数 , k ≠0 ) 的函数叫做反比例函数.kx—1. 什么是函数的图象?建立平面直角坐标系,以自变量取的每一个值为横坐标,相应的函数值为纵坐标,描出对应的点,由所有这些点组成的图形称为这个函数的图象一次函数的图象是一条直线2. 一次函数 的图象是什么样子?(0)ykxb k x画出反比例函数 和的函数图象。 函数图象画法列表描点连线y = x6y = x6 描点法xy66yx123456-1-3-2-4-5-61234-1-2-3-40-6-556yx xy = x6y = x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5 -2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……y = x6y = x6你认为作反比例函数图象时应注意哪些问题?1. 列表时 , 选取的自变量的值 , 既要易于计算 , 又要便于描点 , 尽量多取一些数值 ( 取互为相反数的一对一对的数 ), 多描一些点 , 这样既可以方便连线,又可以使图象精确.2. 描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.3. 一定要按自变量从小到大的顺序依次连线 , 连线时必须用光滑的曲线连接各点 , 不能用折线连接.4. 图象是延伸的,注意不要画得有明确端点.5. 曲线的发展趋势只能靠近坐标轴 , 但不能和坐标轴相交 .【解析】 1 .列表:2 .描点:3 .连线: x… -8 -4 -3 -2 -1…12348……342121-1-2-4-88421213421以表中各组对应值作为点的坐标 , 在平面直角坐标系内描出相应的点 .用光滑的曲线顺次连接各点 , 就可得到图象 .画反比例函数 y = - — 的图象 4x【跟踪训练】4yx123456-4-1-2.-3-5-61 245 63-6 -5-1-3-4-20..... yx...... y = — -4x位置 : 函数 的两支曲线分别位于第一、三象限内 ;函数 的两支曲线分别位于第二、四象限内 .4yx【结论】形状: 反比例函数的图象是由两支曲线组成的 . 因此,称反比例函数的图象为双曲线 .4yx2. 反比例函数 的图象在哪两个象限?由什么确定?kyx当 k>0 时 , 两支曲线...