圆锥曲线的性质复习 江苏省通州市高二数学直线与圆锥曲线课件集 人教版 江苏省通州市高二数学直线与圆锥曲线课件集 人教版VIP免费

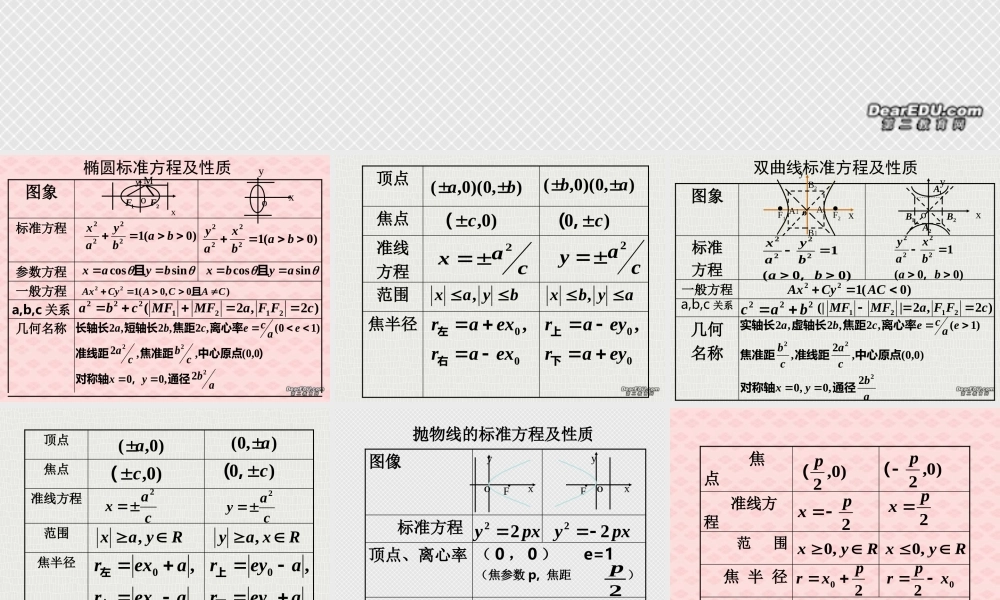
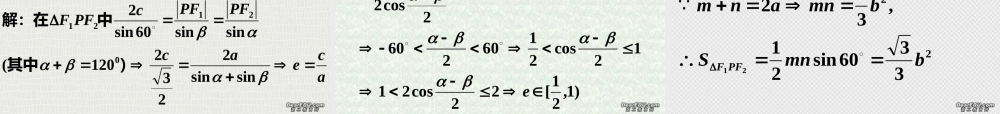椭圆标准方程及性质标准方程几何名称a,b,c 关系一般方程参数方程图象x y)0(12222babyax)0(12222babxay)0,0(122CACACyAx且)2,2(2121222cFFaMFMFcbasincosbyax且sincosaybx且abyxcbcaeacecba2222,000,0(,,2)10(,2,2,2通径，对称轴）中心原点焦准距准线距离心率焦距短轴长长轴长xyooM1F2F焦半径范围准线方程焦点顶点),0)(0,(ba),0)(0,(ab)0,c（)0c，（cax2cay2byax ,aybx ,00,exarexar右左00,eyareyar下上双曲线标准方程及性质几何名称a,b,c 关系一般方程标准方程图象)00(12222babyax，)00(12222babxay，)0(122ACCyAx222bacoxy..F1F2A2A1B2B1abyxcacbeacecba2222,0,0)0,0(,2,)1(,2,2,2通径对称轴中心原点准线距焦准距离心率焦距虚轴长实轴长xyo1B2B1A2A)2,2|(|2121cFFaMFMF焦半径渐近线范围准线方程焦点顶点)0,( a),0(a)0,c（)0c，（cax2cay2Ryax ,aexraexr00,右左Rxay ,aeyraeyr00,下上0aybx0byax 向 左 向 右 开口方向 x 轴 （ y=0 ） 对称轴（ 0 ， 0 ） e=1（焦参数 p, 焦距 ）顶点、离心率 标准方程图像抛物线的标准方程及性质yxOFpxy22 pxy222pxOFy2p( 过焦点的最短弦 ) 通 径 焦 半 径 范 围 准线方程 焦 点)0,2p（)0,2p（2px2px Ryx ,0Ryx ,020pxr02xpr过焦点的弦长221sin2 ppxx221sin2 ppxx 向 下 向 上 开口方向 y 轴 （ x=0 ） 对称轴（ 0 ， 0 ） e=1（焦参数 p, 焦距 ）顶点、离心率 标准方程图像OxFypyx22 pyx22yxOF2p2p( 过焦点的最短弦 ) 通 径 焦 半 径 范 围 准线方程 焦 点)2,0 p（)2,0p（2py2py Rxy ,0Rxy ,020pyr02ypr过焦点的弦长221sin2ppyy221sin2ppyy为例以抛物线)0(22ppxy）。焦点径的圆必过定点为半点为圆心，）以（三点共线；；；）则（，且、过焦点的弦FAAABOARtFBApyypxxyxByxAAB(4,,)3()2(,41),()(,111112212212211).0,2(,2pABOBOA过定点则、若ABFO1A1B。时，动点轨迹为抛物线）当（。时，动点轨迹为双曲线〉）当（时，动点轨迹为椭圆。）当（是一个常数离与到定直线距离之比平面上动点到...