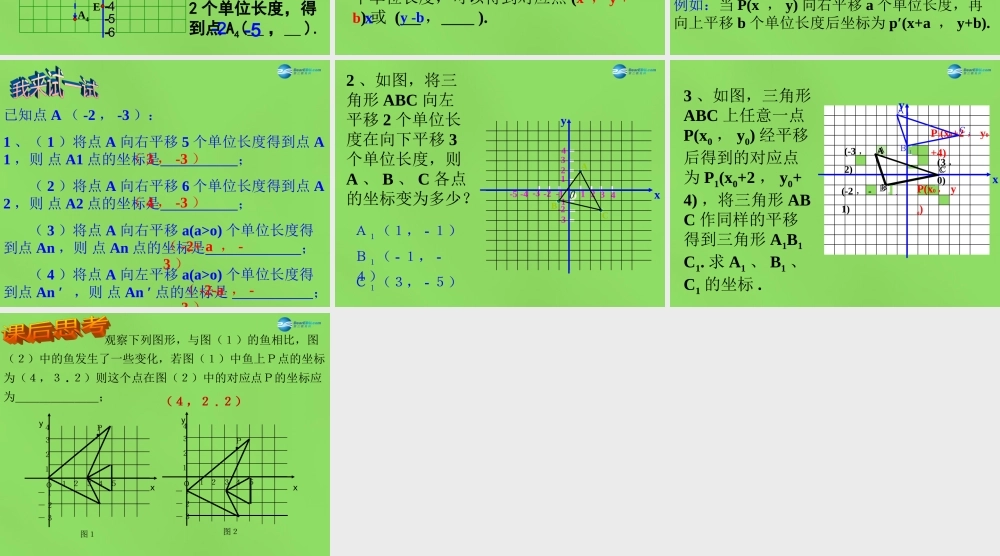
复习回顾-3 -2 -1 0123 xy132-2-1-3ABDC1 . 写出点A、B、C、D的坐标 .A (2,3)B ( - 3, - 3)C (0,2)D ( - 1,0) 2. 下列各点分别在坐标平面的什么位置上?A ( 3 , 2 )B ( 0 ,- 2 )C (- 3 ,- 2 )D (- 3 , 0 )E (- 1.5 , 3.5 )F ( 2 ,- 3 )第一象限第一象限第三象限第三象限第二象限第二象限第四象限第四象限yy 轴上轴上xx 轴上轴上(+ (+ , ,+)+)(- (- , ,+)+)(- (- , , -)-)(+ (+ , , -)-)(0 (0 , ,y)y)(x(x , ,0)0)每个象限内的点都有自已的符号特征每个象限内的点都有自已的符号特征 ..探究AA113355224466--11--22--33--44--55--6600E33 4422--1155--22--33--44--66 --556600 111 、如图: 1 、将点A(-2 , -3) 向右平移 5 个单位长度,得到点 A1( , ) ; 2 、将点 A(-2 , -3) 向左平移 2 个单位长度,得到点 A2( , ) ;A1-4-33-3 A2你发现了什么?你发现了什么?探究AA113355224466--11--22--33--44--55--6600E33 4422--1155--22--33--44--66 --556600 113 、将点 A(-2 , -3) 向上平移 4 个单位长度,得到点 A3( , ) ;4 、将点 A(-2 , -3) 向下平移2 个单位长度,得到点 A4( , ).A3A4-21-2-5你发现了什么?你发现了什么? 2 、将点 (x , y) 向上 ( 或下 ) 平移 b个单位长度,可以得到对应点 (x , y +b) 或 ( , ). 1 、将点 (x , y) 向右 ( 或左 ) 平移 a个单位长度,可以得到对应点 (x+a ,y) 或 ( , ).归纳在平面直角坐标系中,x - ayxy -b 左、右平移纵坐标不变,横坐标变,变化规律是左减右加 ;一个图形在平面直角坐标系中进行平移,其坐 标就要发生相应的变化, 可以简单地理解为:例如:当 P(x , y) 向右平移 a 个单位长度,再向上平移 b 个单位长度后坐标为 p′(x+a , y+b). 上下平移横坐标不变,纵坐标变,变化规律是上加下减 .探究已知点 A ( -2 , -3 ):1 、( 1 )将点 A 向右平移 5 个单位长度得到点 A1 ,则 点 A1 点的坐标是 ; ( 2 )将点 A 向右平移 6 个单位长度得到点 A2 ,则 点 A2 点的坐标是 ; ( 3 )将点 A 向右平移 a(a>o) 个单位长度得到点 An ,则 点 An 点的坐标是 ; ( 4 )将点 A 向...