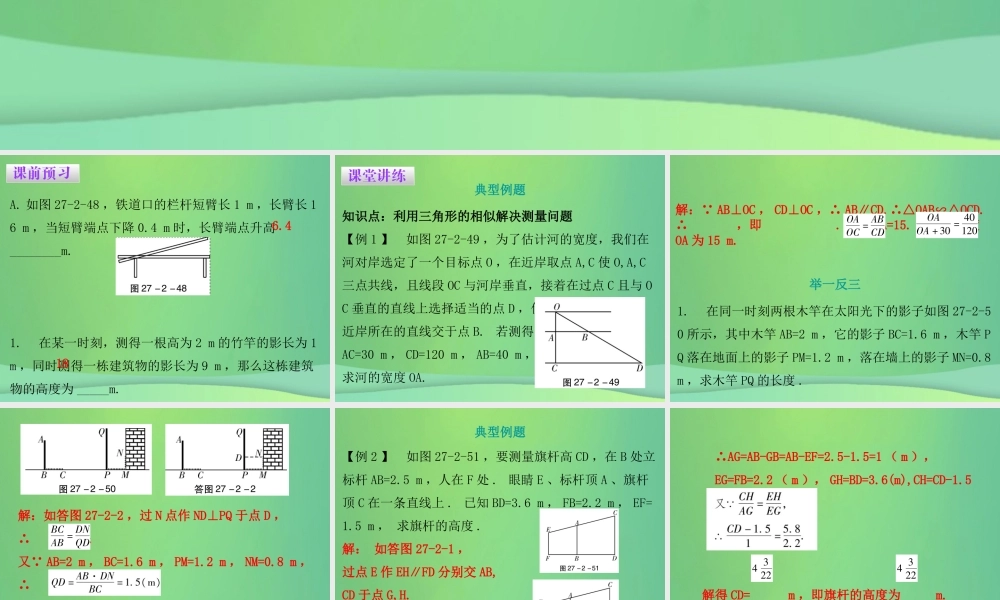
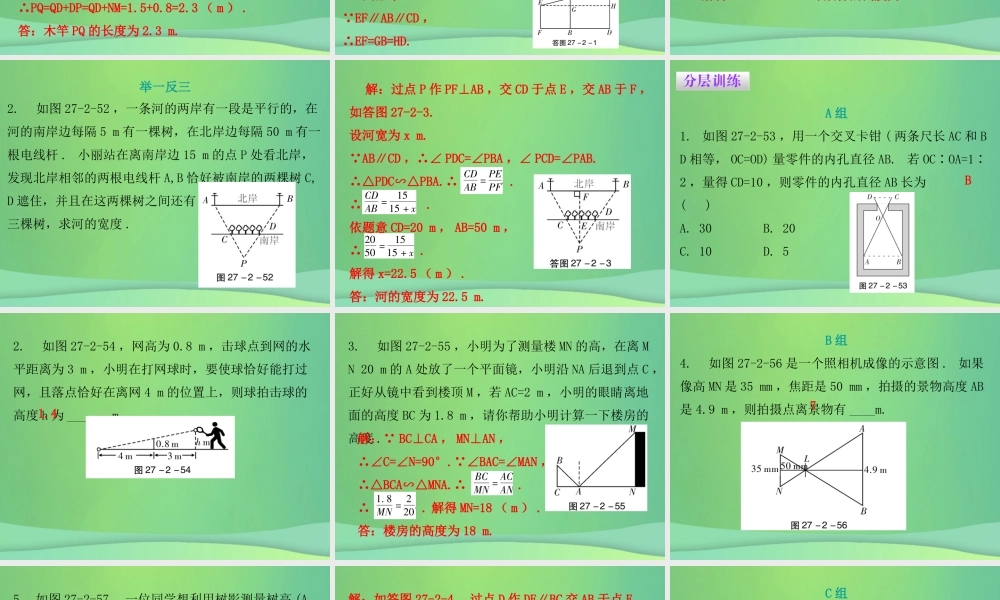
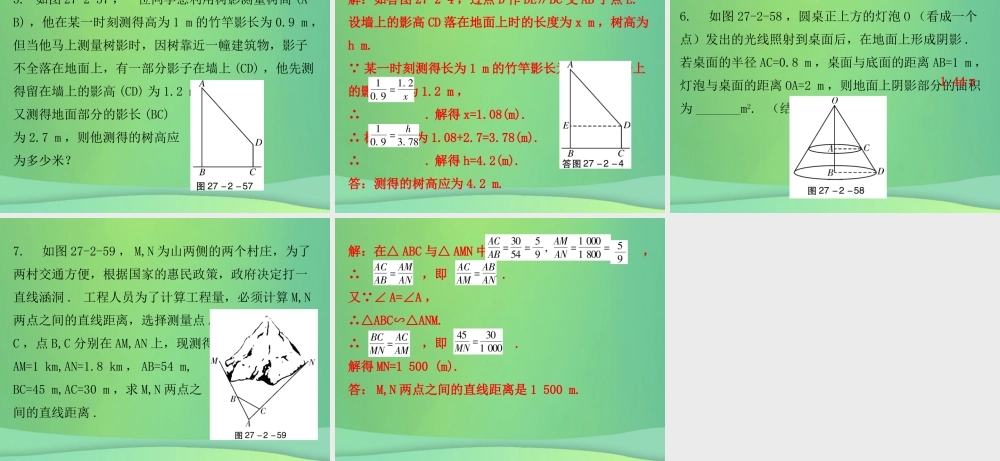
第二十七章相似27.2 相似三角形第 5 课时 相似三角形应用举例数学 九年级 下册 配人教版课前预习A. 如图 27-2-48 ,铁道口的栏杆短臂长 1 m ,长臂长 16 m ,当短臂端点下降 0.4 m 时,长臂端点升高________m.1. 在某一时刻,测得一根高为 2 m 的竹竿的影长为 1 m ,同时测得一栋建筑物的影长为 9 m ,那么这栋建筑物的高度为 _____m.6.418课堂讲练典型例题知识点:利用三角形的相似解决测量问题 【例 1 】 如图 27-2-49 ,为了估计河的宽度,我们在河对岸选定了一个目标点 O ,在近岸取点 A,C 使 O,A,C三点共线,且线段 OC 与河岸垂直,接着在过点 C 且与 OC 垂直的直线上选择适当的点 D ,使 OD 与近岸所在的直线交于点 B. 若测得AC=30 m , CD=120 m , AB=40 m ,求河的宽度 OA.1. 在同一时刻两根木竿在太阳光下的影子如图 27-2-50 所示,其中木竿 AB=2 m ,它的影子 BC=1.6 m ,木竿 PQ 落在地面上的影子 PM=1.2 m ,落在墙上的影子 MN=0.8 m ,求木竿 PQ 的长度 . 解: AB⊥OC , CD⊥OC ,∴ AB∥CD.∴△OAB∽△OCD.∴ ,即 . 解得 OA=15. 故河的宽度OA 为 15 m.举一反三解:如答图 27-2-2 ,过 N 点作 ND⊥PQ 于点 D ,∴ .又 AB=2 m , BC=1.6 m , PM=1.2 m , NM=0.8 m ,∴ .∴PQ=QD+DP=QD+NM=1.5+0.8=2.3 ( m ) .答:木竿 PQ 的长度为 2.3 m. 【例 2 】 如图 27-2-51 ,要测量旗杆高 CD ,在 B 处立标杆 AB=2.5 m ,人在 F 处 . 眼睛 E 、标杆顶 A 、旗杆顶 C 在一条直线上 . 已知 BD=3.6 m , FB=2.2 m , EF=1.5 m , 求旗杆的高度 .解: 如答图 27-2-1 ,过点 E 作 EH∥FD 分别交 AB,CD 于点 G,H. EF∥AB∥CD ,∴EF=GB=HD.典型例题 ∴AG=AB-GB=AB-EF=2.5-1.5=1 ( m ), EG=FB=2.2 ( m ), GH=BD=3.6(m),CH=CD-1.5( m ) .解得 CD= m ,即旗杆的高度为 m. 2. 如图 27-2-52 ,一条河的两岸有一段是平行的,在河的南岸边每隔 5 m 有一棵树,在北岸边每隔 50 m 有一根电线杆 . 小丽站在离南岸边 15 m 的点 P 处看北岸,发现北岸相邻的两根电线杆 A,B 恰好被南岸的两棵树 C,D 遮住,并且在这两棵树之间还有三棵树,求河的宽度 .举一反三 解:过点 P 作 PF⊥AB ,交 CD 于点 E ,交 AB...