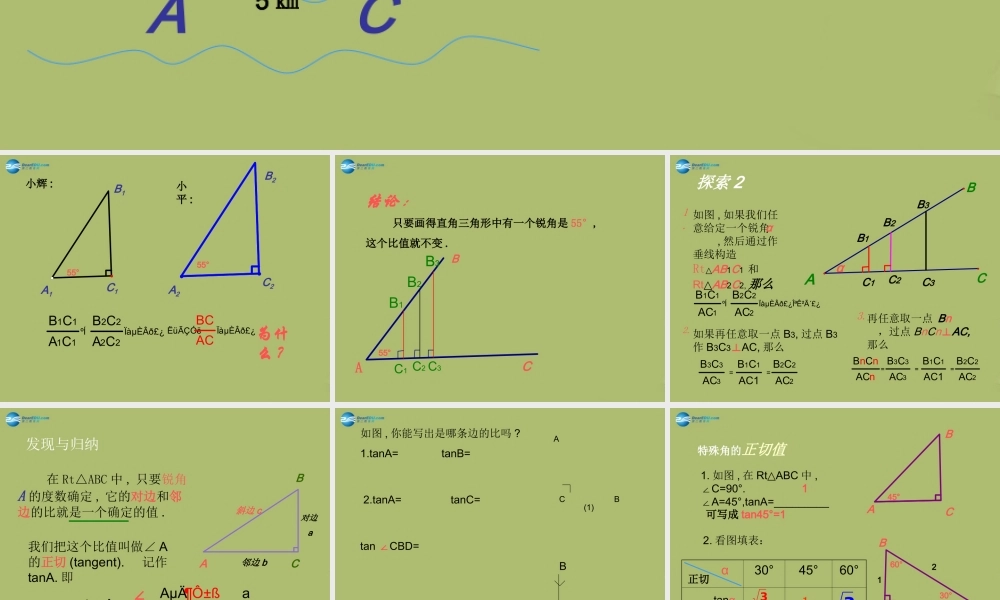
探索 1 一艘轮船航行到 A 处时 , 灯塔 B 位于它的北偏东 35° 的方向上 , 轮船向东又航行 5 ㎞到达 C 处时 ,灯塔在轮船的正北方 ( 如图 ), 请你想一想用什么办法能求出这时轮船到灯塔的距离 .35°5 ㎞ABC55°55°B2C2A2A1B1C1小辉 :小平 :B1C1A1C1ºÍ B2C2A2C2ÏàµÈÂ𣿠ËüÃÇÓëBCACÏàµÈÂð£¿为什么 ?结论 : 只要画得直角三角形中有一个锐角是 55°,这个比值就不变 .55°AB1C1B2B3C2 C3B3BC探索 2AB1C1C2C3BnB3B2BCα如图 , 如果我们任意给定一个锐角 , 然后通过作垂线构造Rt△AB1C1 和Rt△AB2C2, 那么αB1C1AC1ºÍ B2C2AC2ÏàµÈÂð£¿ÎªÊ²Ã´£¿如果再任意取一点 B3, 过点 B3作 B3C3⊥AC, 那么B3C3AC3 = B1C1AC1 = B2C2AC2 再任意取一点 ,过点 BnCn⊥AC,那么BnCnACn= B3C3AC3 = B1C1AC1 = B2C2AC2 1.2.3.发现与归纳 在 Rt△ABC 中 , 只要锐角A 的度数确定 , 它的对边和邻边的比就是一个确定的值 .我们把这个比值叫做∠ A的正切 (tangent). 记作tanA. 即 ACB邻边 b斜边 ctanA = AµÄ¶Ô±ß AµÄÁÚ±ß = ab∠∠对边 a如图 , 你能写出是哪条边的比吗 ?1.tanA= tanB= 2.tanA= tanC=tan ∠CBD= ABC(1)A BDCtan∠ABD=特殊角的正切值1. 如图 , 在 Rt ABC△中 , C=90°. ∠A=45°,tanA=_________∠ACB45°可写成 tan45°=12. 看图填表:30°45°60°αtanα3133CAB30°60°123正切1用一用 1. 如图所示 ,Rt ABC△中 , ∠C=90. AC=4,BC=8, 则 tanB= . 2. △ABC 中 , ∠C=90°,AB=15,BC=12, 则 tanA 等于__________ . 3. 在 RtABC 中 , ∠C=90°,tanA= , 若把 Rt△ ABC 三边都扩大 2 倍后 , 得到 Rt A′B′C′,△则 . tanA′=______′12ABC484312124. 已知 α 为锐角 , 且 tan(90-α )= , 则的 α 度数为 ( )A.30 B.45 C.60 D.755. 如图所示 , 点 P 在第二象限 ,OP=5,tan = 则点 P 的坐标为 _________ .3α43xyopαA(-3,4)作业选做 : 研究一下在 Rt ABC△中 , 当锐角度数确定时还有哪些边的比值确定 ? 这些比值有何关系 ?