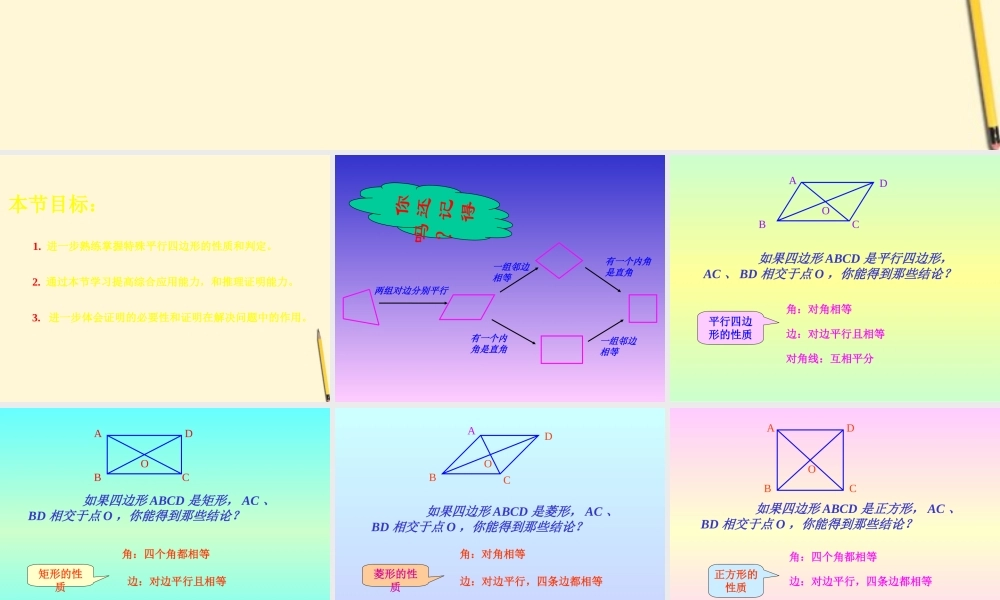
本节目标:1. 进一步熟练掌握特殊平行四边形的性质和判定。2. 通过本节学习提高综合应用能力,和推理证明能力。3. 进一步体会证明的必要性和证明在解决问题中的作用。 两组对边分别平行 一组邻边相等有一个内角是直角一组邻边相等有一个内角是直角你还记得吗? 如果四边形 ABCD 是平行四边形,AC 、 BD 相交于点 O ,你能得到那些结论?ABCDO角:对角相等边:对边平行且相等对角线:互相平分平行四边形的性质 ABCDO角:四个角都相等边:对边平行且相等对角线:互相平分且相等矩形的性质 如果四边形 ABCD 是矩形, AC 、BD 相交于点 O ,你能得到那些结论? 如果四边形 ABCD 是菱形, AC 、BD 相交于点 O ,你能得到那些结论?ABCDO角:对角相等边:对边平行,四条边都相等对角线:互相垂直平分菱形的性质 ABCDO角:四个角都相等边:对边平行,四条边都相等正方形的性质 如果四边形 ABCD 是正方形, AC 、BD 相交于点 O ,你能得到那些结论?对角线:互相垂直平分且相等 (1) AB=CD(2) AD=BC(3) AB=BC(4) AB CD∥(5) AD BC∥(6) BAD=BCD∠∠(7) ABC=ADC∠∠(8) BAD=90∠。(9) OA=OC(10) OB=OD(11) ACBD⊥(12) AC=BD边角对角线 你能在四边形的基础上 , 从下列条件中选三个 , 得到矩形吗 ?ABCDO 你能在四边形的基础上 ,从下列条件中选三个 , 得到菱形吗 ?(1) AB=CD(2) AD=BC(3) AB=BC(4) AB CD∥(5) AD BC∥(6) BAD=BCD∠∠(7) ABC=ADC∠∠(8) BAD=90∠。(9) OA=OC(10) OB=OD(11) ACBD⊥(12) AC=BD边角对角线ABCDO 你能在四边形的基础上 , 从下列条件中选四个 , 得到正方形吗 ?(1) AB=CD(2) AD=BC(3) AB=BC(4) AB CD∥(5) AD BC∥(6) BAD=BCD∠∠(7) ABC=ADC∠∠(8) BAD=90∠。(9) OA=OC(10) OB=OD(11) ACBD⊥(12) AC=BD边角对角线ABCDO 1. 平行四边形的一个角是另一个角的 5 倍,这个平行四边形较大的角是——2. 已知平行四边形的周长是 30cm ,两邻边之比为 1 : 5 ,那么较小边的边长为——3. 已知:如图( 1 )在菱形 ABCD 中, E 、 F 分别是 BC 、 CD上的点,且 AE=EF=AF=AB ,则∠ C=——4. 已知菱形的一边和等腰直角三角形的直角边相等,若菱形的一角为 60º ,则菱形和三角形的面积比是——5. 如图( 2 ),在正方形 ABCD 中,延长 BC 至 E ,使 CE=AC , AE 交CD 于 F ,那么∠ AFC=—...